Приведение вторичной обмотки к первичной
Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если у первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков.
Представим себе, что реальная вторичная обмотка трансформатора с числом витков w2 заменена воображаемой, или приведенной, обмоткой с числом витков w2’ = w1. При этом число витков вторичной обмотки изменится в
| (1) |
раз. Величина k называется коэффициентом приведения или коэффициентом трансформации. Более подробно о том, что называется коэффициентом трансформации и как определить коэффициент трансформации изложено в статье "Принцип действия и виды трансформаторов".
В результате такой замены, или приведения, электродвижущая сила E2’ и напряжение U2’ приведенной обмотки также изменяются в k раз по сравнению с величинами E2 и U2 реальной вторичной обмотки:
| (2) |
Чтобы мощности приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство
![]()
где I2’ – приведенный вторичный ток. Отсюда с учетом второго равенства (2) следует, что
| (3) |
Намагничивающие силы приведенной и реальной обмоток на основании выражений (1) и (3) равны:
| (4) |
Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого, кроме соблюдения условия (4), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне магнитопровода трансформатора так же, как и реальная вторичная обмотка (смотрите например, рисунок 1, в статье "Магнитопроводы трансформаторов" и рисунок 1, в статье "Элементы конструкции и способы охлаждения масляных трансформаторов"). Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в k раз. Но поскольку приведенная обмотка имеет в k раз больше витков, то в итоге активное сопротивление приведенной обмотки в k2 раз больше, чем реальной:
| (5) |
Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки x2’ и реальной x2 существует такое же соотношение:
| (6) |
Очевидно, что потери в приведенной и реальной обмотках одинаковы:
![]()
Одинаковы также относительные падения напряжения во вторичных обмотках приведенного и реального трансформаторов:
![]()
Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.
Схема замещения без учета магнитных потерь
В соответствии с изложенным сделаем подстановки в уравнениях напряжения трансформатора (уравнения (2), представленные в статье "Уравнения напряжений трансформатора"):
| (7) |
что в математическом отношении соответствует переходу от исходных реальных переменных U2, I2 к новым (приведенным) переменным U2’, I2’. Умножив при этом второе из уравнений (2), представленное в статье "Уравнения напряжений трансформатора", на k, получим
| (8) |
При переходе к электрической связи двух цепей в соответствующей схеме замещения должна появиться общая для обеих цепей ветвь, которая обтекается суммой токов обеих цепей I1 + I2’. Соответственно этому в уравнениях напряжений этих цепей должны появиться одинаковые члены с множителями (I1 + I2’). Из уравнений (8) видно, что для получения в них таких членов нужно прибавить к первому из этих уравнений и вычесть из него член jkx12 × I1 и прибавить ко второму и вычесть из него член jkx12 × I2’. При этом получим
| (9) |
Введем следующие наименования и обозначения:
1) приведенное активное сопротивление вторичной обмотки
| (10) |
совпадающее с выражением (5);
2) приведенное взаимное индуктивное сопротивление
| (11) |
3) индуктивное сопротивление рассеяния первичной обмотки
| (12) |
4) приведенное индуктивное сопротивление рассеяния вторичной обмотки
| (13) |
где
| (14) |
представляет собой неприведенное индуктивное сопротивление рассеяния вторичной обмотки.
Введя перечисленные приведенные величины в уравнения (9), получим уравнения напряжения приведенного трансформатора:
| (15) |
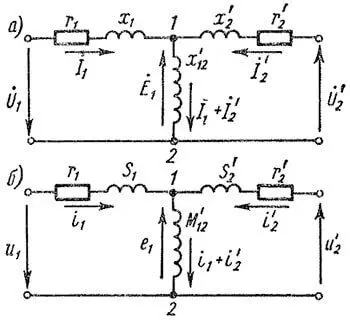 |
| Рисунок 1. Схемы замещения двухобмоточного трансформатора без учета магнитных потерь |
Уравнениям (15), как нетрудно видеть, соответствует схема замещения рисунка 1, а. Действительно, мысленно обойдя левый и правый контуры схемы рисунка 1, а и составив уравнения напряжения для этих контуров, вновь получим уравнения (15). Таким образом, схема рисунка 1, а представляет собой схему замещения трансформатора, соответствующую уравнению (2), представленному в статье "Уравнения напряжений трансформатора" и уравнению (15), представленному в данной статье.
Аналогичным образом можно также преобразовать уравнения напряжения в дифференциальной форме (уравнения (1), представленные в статье "Уравнения напряжений трансформатора"), произведя в них подстановки
| u2 = u2’ / k ; i2 = k × i2’ . | (16) |
При этом получается схема замещения рисунка 1, б, где
| (17) |
и
| (18) |
представляют собой индуктивности рассеяния первичной и вторичной обмоток, а
| (19) |
– приведенную взаимную индуктивность.
Схема замещения рисунка 1, б действительна при любых закономерностях изменения напряжения и токов во времени, в том числе и в случае переходных процессов.
Уравнения (15) и схемы замещения рисунка 1 можно трактовать таким образом, что сопротивления r1 и x1, r2’ и x2’ или индуктивности S1 и S2’ включены в цепи обмоток до и после трансформатора, а параметры обмоток трансформатора уменьшены на значения этих величин. В результате получается идеальный трансформатор, активные сопротивления которого равны нулю, а коэффициент электромагнитной связи c = 1. Действительно, у такого идеального трансформатора приведенные собственные и взаимные индуктивные сопротивления одинаковы и равны x12’ = k × x12 и поэтому в соответствии с равенством (12), представленном в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние" и равенством (7), представленном в статье "Уравнения напряжений трансформатора", c2 = 1 и σ = 0.
Отметим, что, как следует из рассмотрения приведенных преобразований, соотношения (7) и все последующие, а также схемы замещения рисунка 1 справедливы и правильно отражают все процессы в трансформаторе при любом значении k. С математической точки зрения эти преобразования означают переход от переменных U2 и I2 к новым переменным U2’ и I2’ по формулам (7), что возможно при любом значении k. В связи с этим необходимо подчеркнуть, что индуктивные сопротивления и индуктивности рассеяния, согласно равенствам (11) – (14), (17), (18) и (19), определяются неоднозначно и зависят от коэффициента приведения k. Однако для силовых трансформаторов k рационально определять по формуле (1), как это и принято на практике. Выбор иного значения k целесообразен лишь в специальных случаях, например в измерительных трансформаторах тока.
Параметры схемы замещения
Рассмотрим параметры схем замещения рисунка 1 при k = w1 / w2 [смотрите равенство (1)].
Приведенная взаимная индуктивность на основании равенств (6) и (10), в представленных статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние" и равенства (19), настоящей статьи
![]()
или на основании выражения (4), в представленного в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние"
| (20) |
Последний член выражения (20) весьма мал по сравнению с первым, и поэтому с достаточной точностью
| M12’ ≈ Lс1 . | (21) |
Соответственно, согласно выражению (3), представленного в статье "Уравнения напряжений трансформатора" и выражениям (11), (19), (21), настоящей статьи,
x12’ = k × x12 = ω × k × M = ω × M12’ ≈ ω × Lс1
или
| x12’ ≈ xс1 = ω × w12 / Rµc . | (22) |
Следовательно, сопротивление x12’ с большой точностью равно сопротивлению самоиндукции первичной обмотки от потока, замыкающегося по магнитопроводу.
Ветви 1 – 2 схем замещения рисунка 1 называются намагничивающими ветвями. Протекающий по этим ветвям намагничивающий ток
|
создает результирующую намагничивающую силу обмоток трансформатора
Fрез = w1 × (I1 + I2’) = w1 × I1 + w1 × I2’ = F1 + F2 ,
которая в свою очередь создает результирующий поток стержня с амплитудой Фс. Напряжение на этих ветвях в соответствии с выражением (22), настоящей статьи и выражением (3), представленным в статье "Принцип действия и виды трансформаторов"
![]()
![]()
то есть равно по значению и обратно по знаку электродвижущей силе E1, которая индуктируется в первичной обмотке результирующим потоком магнитопровода, или основным потоком трансформатора, и отстает от него на 90°.
Индуктивность рассеяния первичной обмотки, согласно выражениям (9) и (10), представленных в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние" и выражению (17), данной статьи,
S1 = L11 – k × M = Lc1 + Lв1 – k × Mc – k × Mв .
Но на основании уравнений (4) и (6), представленных в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние"
![]()
Поэтому
| S1 = Lв1 – k × Mв . | (23) |
Аналогично, согласно выражениям (9) и (10), представленных в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние" и выражению (18), данной статьи
![]()
Но основании уравнений (5) и (6), представленных в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние"
![]()
и поэтому
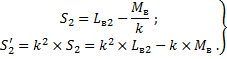 | (24) |
Таким образом, индуктивности рассеяния S1, S2 и S2’ и индуктивные сопротивления рассеяния при k = w1 / w2 определяются магнитными потоками, замыкающимися главным образом по воздуху.
| (25) |
Однако вторыми членами равенств (23) и (24) по сравнению с первыми пренебречь нельзя, и поэтому потоки, замыкающиеся по воздуху, можно назвать потоками рассеяния лишь условно.
Схема замещения с учетом магнитных потерь
Потери в стали магнитопровода pмг при заданной частоте пропорциональны следующим величинам:
pмг ∼ Bc2 ∼ Фc2 ∼ E12 .
Таким образом, потери pмг пропорциональны квадрату напряжения U12 на зажимах 1 – 2 намагничивающей цепи схемы замещения рисунка 1, а. Если к этим зажимам параллельно x12’ = xc1 подключить активное сопротивление rмг, как показано на рисунке 2, а, то потери в этом сопротивлении также будут пропорциональны U12. Значение сопротивления rмг можно подобрать так, чтобы потери в нем равнялись магнитным потерям:
pмг = m1 × U122 / rмг = m1 × E12 / rмг .
Отсюда
| rмг = m1 × E12 / pмг . | (26) |
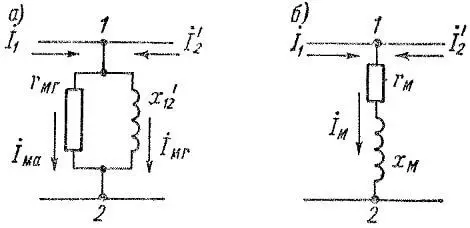
Рисунок 2. Намагничивающая цепь схемы замещения с учетом магнитных потерь
Величину pмг при заданной электродвижущей силе E1 можно считать известной из расчетных (смотрите статью "Расчет магнитной цепи трансформатора") или опытных данных. Тогда можно считать известным также rмг.
Намагничивающий ток
![]()
разделяется в двух ветвях намагничивающей цепи (рисунок 2, а) на активную Iмa и реактивную Iмr составляющие (смотрите статью "Расчет магнитной цепи трансформатора"), из, из которых первая определяет мощность магнитных потерь, а вторая создает поток магнитопровода.
Схема с двумя параллельными ветвями намагничивающей цепи хорошо согласуется с реальными физическими явлениями. Однако расчеты на основе схемы замещения вести удобнее, если объединить две параллельные ветви схемы 2, а в одну общую ветвь, как показано на рисунке 2, б. Тогда сопротивление этой ветви
| (27) |
Так как rмг >> x12’, то
| (28) |
При увеличении насыщения магнитопровода, то есть при увеличении Фс, E1 или U1, сопротивление x12’ при f = const уменьшается. Однако при этом rмг ≈ const, а значение rм уменьшается.
Схема замещения трансформатора с учетом магнитных потерь согласно рисунку 2, б показана на рисунке 3, а. Если использовать обозначения
| Z1 = r1 + jx1 ; Z2’ = r2’ + jx2’ ; Zм = rм + jxм , | (29) |
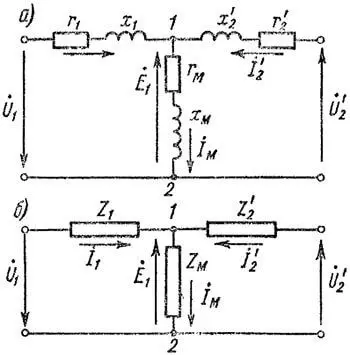 |
| Рисунок 3. Схема замещения двухобмоточного трансформатора с учетом магнитных потерь |
то схему замещения можно изобразить более компактно, как показано на рисунке 3, б. В режиме холостого хода I2’ = 0 и I1 = Iм – току холостого хода трансформатора.
В итоге получилась весьма простая Т-образная схема замещения трансформатора, представляющая собой пассивный четырехполюсник. Сопротивление намагничивающей цепи этой схемы Zм отражает явления в ферромагнитном магнитопроводе. Оно значительно больше сопротивлений Z1 и Z2’, которые включают в себя активные сопротивления и индуктивные сопротивления рассеяния обмоток. Для силовых трансформаторов в относительных единицах
zм* = 25 – 200 ; z1* ≈ z2*’ = 0,025 – 0,10 .
Уравнения напряжений и схему замещения трансформатора можно представлять также в относительных единицах. Имея в виду, что
Uн = zн × Iн ,
левые части уравнений вида (15) можно разделить на Uн, а правые части – на Zн × Iн, в результате чего и будет совершен переход к относительным единицам. Абсолютные значения U, I, r, x и Z в схемах замещения также можно заменить относительными. При этом расчеты режимов работы трансформатора можно вести в относительных единицах.
Нетрудно видеть, что относительные значения сопротивлений, токов и напряжений вторичной цепи будут зависеть от того, какая величина коэффициента k была использована при приведении вторичной обмотки к первичной. Неопределенность в этом вопросе исчезает, если определять k всегда одинаковым образом. Например, в силовых трансформаторах всегда берут k = w1 / w2.
Упрощенная схема замещения
 |
| Рисунок 4. Упрощенная схема замещения трансформатора |
Так как Zм >> Z1 ≈ Z2’, то во многих случаях можно положить Zм = ∞, что означает разрыв намагничивающей цепи схемы замещения рисунка 3. При Zм = ∞ будет Iм = 0, то есть такое предположение эквивалентно пренебрежению намагничивающим током или током холостого хода, что ввиду малости Iм во многих случаях допустимо. При этом I1 = –I2’ = I .
При Zм = ∞ и Iм = 0 схема замещения принимает вид, изображенный на рисунке 4. Параметры этой схемы
| (30) |
называются соответственно полным, активным и индуктивным сопротивлениями короткого замыкания. Такие названия обусловлены тем, что замыкание вторичных зажимов трансформатора накоротко соответствует замыканию накоротко вторичных (правых) зажимов схемы замещения рисунка 4 и при этом сопротивление трансформатора при коротком замыкании будет равным Zк.
Схема замещения рисунка 4 чрезвычайно проста. Согласно этой схеме, трансформатор эквивалентен сопротивлению Zк. Обычно в силовых трансформаторах zк* = 0,05 – 0,15.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.