Закон полного тока

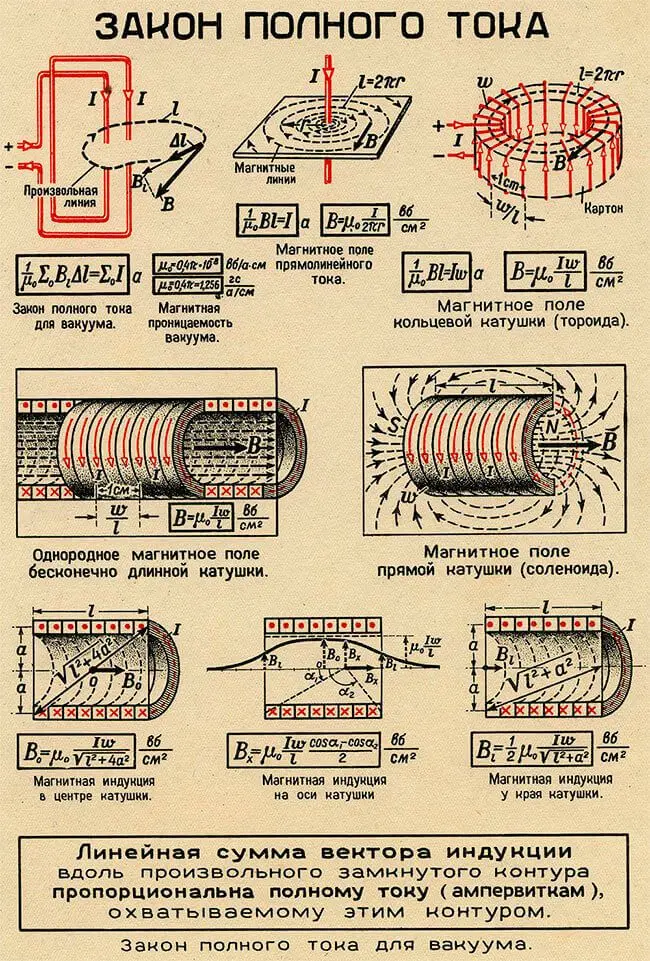
Пусть произвольная замкнутая линия l пронизывает проводник с током (рисунок 1), то есть они сцепляются друг с другом как два звена цепи. Вокруг проводника возникает магнитное поле.

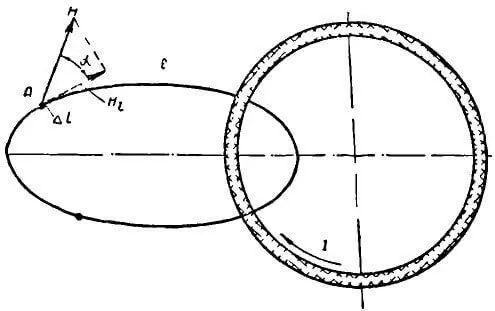
Рисунок 1. Закон полного тока

Построим вектор напряженности H, создаваемой током в точке А, расположенной на линии l. Если линия охватывает несколько проводников с током, то для каждого тока строятся векторы напряженности в данной точке линии. Складывая геометрически отдельные векторы напряженности, находим вектор результирующей напряженности магнитного поля.

Вектор результирующей напряженности H в общем случае образует с элементом длины Δl угол α. Поэтому продольная или тангенциальная составляющая H_l результирующей напряженности H будет:

H_l = H × cos α.

Если разбить замкнутую линию на n элементов длины и сложить произведения длин всех элементов на тангенциальные составляющие результирующей напряженности в этих элементах, получим следующую сумму:

Эту сумму можно представить так:

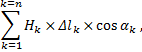
где знак  означает сумму от k = 1 до k = n.

В теоретической электротехнике доказывается, что указанная сумма равна алгебраической сумме токов, сцепляющихся с контуром суммирования подобно тому, как сцепляются между собой два смежных звена цепи.

Следовательно, можно записать так:

Эта формулировка называется законом полного тока. Для случая, когда контур многократно пронизывает один и тот же виток, как, например,  при наличии обмотки с числом витков w, полный ток будет:

Если замкнутый контур суммирования совпадает с магнитной линией, то вектор напряженности в любой точке контура будет направлен по касательной к элементу длины Δl.

В этом случае

и закон полного тока принимает вид:

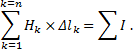
Если значение напряженности для всех точек контура при этом одинаково, а сумма Δl по контуру равна l, то формула закона полного тока запишется так:

Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определять напряженность поля.

Например, применяя закон полного тока для определения напряженности на расстоянии a от прямолинейного проводника с током, имеем:

l = 2 × π × a .

Поэтому

H × 2 × π × a = I ,

откуда

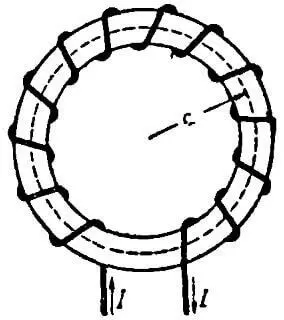Рисунок 2. К определению напряженности поля катушки, намотанной на кольцо

Чтобы определить напряженность поля внутри катушки, намотанной на кольцо (рисунок 2), воспользуемся опять законом полного тока. Контуром здесь является окружность радиуса r. Контур пронизывает w витков с токами одного направления:

H × 2 × π × r = I × w .

Обозначая длину средней линии кольца через l = 2 × π × r , получаем:

H × l = I × w ,

откуда

Таким образом, напряженность поля катушки пропорциональна произведению числа ампер на число витков или числу ампер-витков. I × w называется намагничивающей силой и обозначается буквой F. Так как w – число отвлеченное, то намагничивающая сила измеряется в амперах.

Магнитная индукция внутри катушки будет:

Если площадь поперечного сечения кольца по всей длине одинакова и равна S, то, зная магнитную индукцию B, можно определить магнитный поток Ф:

Эту же формулу можно представить в ином виде:

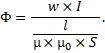
По своему строению эта формула напоминает формулу Ома. Выше было указано, что произведение I × w называется намагничивающей силой. Выражение  стоящее в знаменателе, называется магнитным сопротивлением и обозначается буквой R_м:

Из этой формулы видно, что магнитное сопротивление пропорционально длине пути и обратно пропорционально сечению материала, по которому проходит магнитный поток.

Таким образом, магнитный поток Ф пропорционален намагничивающей силе F и обратно пропорционален магнитному сопротивлению R_м:

Рисунок 3. Закон полного тока для вакуума

Источник: Кузнецов М.И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560с.