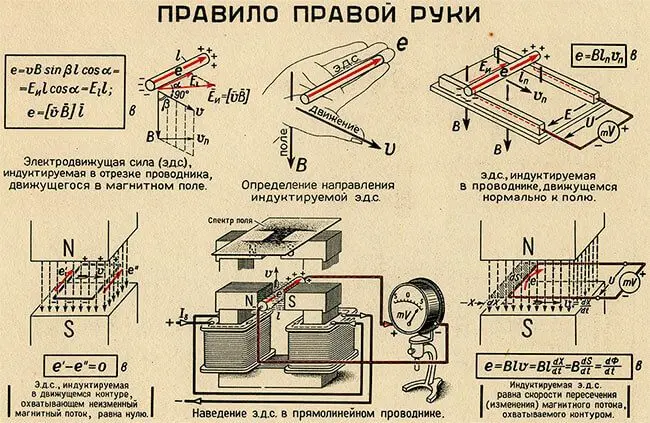
Индуктированная электродвижущая сила (ЭДС) возникает в следующих случаях:
- Когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один относительно другого;
- Когда переменное магнитное поле одного проводника, действуя на другой проводник, индуктирует в нем ЭДС (взаимоиндукция);
- Когда изменяющееся магнитное поле индуктирует в енм самом ЭДС (самоиндукция).
Таким образом, всякое изменение во времени величины магнитного потока, пронизывающего замкнутый контур (виток, рамку), сопровождается появлением в проводнике индуктированной ЭДС.
Как было отмечено в статье "Явление электромагнитной индукции", направление ЭДС магнитной индукции зависит от направления движения проводника и от направления магнитного поля.
Для определения направления индуктированной ЭДС в проводнике служит "правило правой руки". Оно заключается в следующем: если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут указывать направление индуктированной ЭДС в проводнике (рисунок 1).
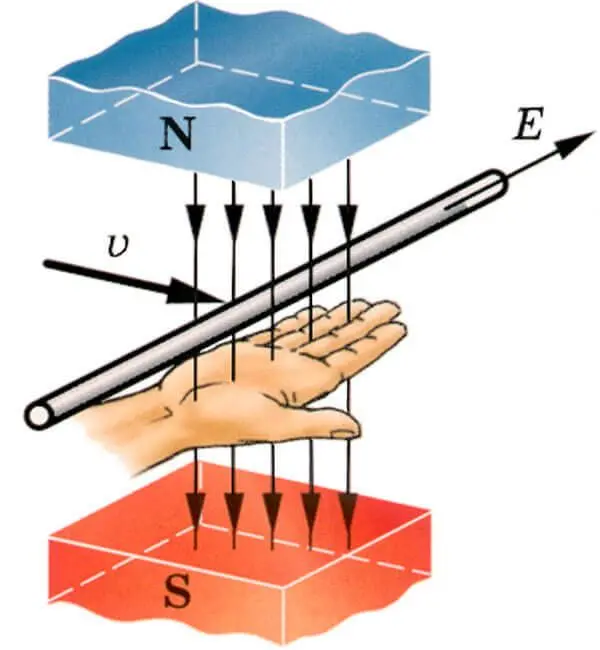
Рисунок 1. Определение направления ЭДС индукции в проводнике по "правилу правой руки"
В случаях, когда проводник остается неподвижным, а магнитное поле движется, для определения направления индуктированной ЭДС нужно предположить, что поле остается неподвижным, а проводник движется в сторону, обратную движению поля, и применить "правило правой руки".
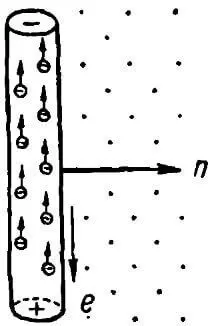 |
| Рисунок 2. Электромагнитная индукция в проводнике |
Явление индуктированной ЭДС можно также объяснить при помощи электронной теории.
Поместим проводник в магнитное поле. Свободные электроны проводника будут находиться в беспорядочном тепловом движении. Положительные и отрицательные заряды равномерно расположены по всему объему проводника и взаимно нейтрализуют друг друга. Будем перемещать проводник с определенной скоростью в однородном магнитном поле в направлении n (рисунок 2) перпендикулярно вектору магнитной индукции. Магнитные линии, показанные точками, направлены из-за плоскости чертежа к читателю.
На электрические заряды проводника в этом случае будет действовать сила, под действием которой свободные электроны получат добавочную составляющую скорости и будут двигаться вдоль проводника.
В то время как положительные заряды, связанные с кристаллической решеткой проводника, относительно проводника не смещаются, движущиеся вместе с проводником свободные электроны могут перемещаться относительно него.
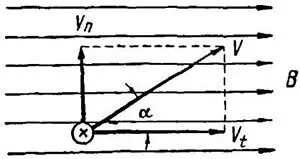 |
| Рисунок 3. Разложение скорости движения проводника в магнитном поле |
В нашем примере электроны движутся от нижнего края проводника к его верхнему краю, что соответствует направлению тока сверху вниз. Направление индуктированной ЭДС и тока в проводнике, как легко убедиться, согласуется с правилом правой руки.
Величина ЭДС индукции магнитного поля в проводнике зависит:
- от величины индукции B магнитного поля, так как чем гуще расположены магнитные индукционные линии, тем больше число их пересечет проводник за единицу времени (секунду);
- от скорости движения проводника v в магнитном поле, так как при большой скорости движения проводник может больше пересечь индукционных линий в секунду;
- от рабочей (находящейся в магнитном поле) длины проводника l, так как длинный проводник может больше пересечь индукционных линий в секунду;
- от величины синуса угла α между направлением движения проводника и направлением магнитного поля (рисунок 3).
Раскладываем вектор скорости движения проводника в магнитном поле на две составляющие: vn – составляющую нормальную к направлению поля (vn = v × sin α) и vt – тангенциальную составляющую (vt = v × cos α), которая не принимает участия в создании ЭДС, так как при движени под воздействием тангенциальной составляющей проводник двигался бы параллельно вектору B и не пересекал бы линии магнитной индукции.
Формула ЭДС индукции дает возможность определить ее величину:
e = B × l × v × sin α (В) .
Познакомившись с явлением электромагнитной индукции, рассмотрим еще раз процесс преобразования электрической энергии в механическую.
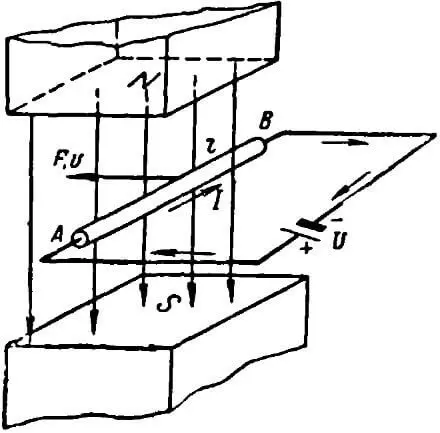
Рисунок 4. Преобразование электрической энергии в механическую
Пусть прямолинейный проводник АВ (рисунок 4), по которому проходит ток от источника напряжения, помещен во внешнее магнитное поле. Если проводник неподвижен, то энергия источника напряжения расходуется исключительно на нагрев проводника:
A = U × I × t = I² × r × t (Дж) .
Затрачиваемая мощность будет равна:
Pэл = U × I = I² × r (Вт) ,
откуда определяем ток в цепи:
| (1) |
Однако нам известно, что проводник с током, помещенный в магнитное поле, будет испытывать силу со стороны поля, стремящуюся перемещать проводник в магнитном поле в направлении, определяемом правилом левой руки. При своем движении проводник будет пересекать магнитные силовые линии поля и в нем по закону электромагнитной индукции возникнет индуктированная ЭДС. Направление этой ЭДС, определенное по правилу правой руки, будет обратным току I. Назовем ее обратной ЭДС Eобр. Величина Eобр согласно закону электромагнитной индукции будет равна:
Eобр = B × l × v (В) .
По второму закону Кирхгофа для замкнутой цепи имеем:
U – Eобр = I × r
или
| U = Eобр + I × r , | (2) |
откуда ток в цепи
| (3) |
Сравнивая выражения (1) и (3), видим, что в проводнике, движущемся в магнитном поле, при одних и тех же значениях U и r ток будет меньше, чем при неподвижном проводнике.
Умножая полученное выражение (2) на I, получим:
U × I = Eобр × I + I² × r .
Так как Eобр = B × l × v, то
U × I = B × l × v × I + I² × r .
Учитывая, что B × l × I = F и F × v = Pмех, имеем:
U × I = F × v + I² × r
или
P = Pмех + Pэм .
Последнее выражение показывает, что при движении проводника с током в магнитном поле мощность источника напряжения преобразуется в тепловую и механическую мощности.
Источник: Кузнецов М. И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560с.