Уравнения напряжений трансформатора

Рабочий процесс трансформатора можно исследовать на основе уравнений напряжений его обмоток.

Уравнения напряжения в дифференциальной форме

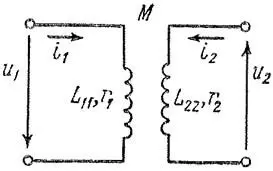
Емкостные токи между элементами обмоток (витки и катушки) и между обмотками и магнитопроводом трансформатора в обычных условиях работы трансформаторов (f < 1 – 5 кГц) весьма малы, и ими можно пренебречь. В трансформаторах без ферромагнитного магнитопровода L₁₁, L₂₂ и M постоянны. В соответствии с изложенным в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние" можно принять, что эти величины постоянны также для любого рассматриваемого режима работы трансформатора со стальным магнитопроводом. Пренебрежем сначала магнитными потерями в магнитопроводе. Тогда для однофазного двухобмоточного трансформатора (рисунок 1) действительны следующие уравнения напряжения в дифференциальной форме:

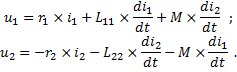(1)

Здесь u₁, u₂, i₁, i₂ – мгновенные значения напряжения и тока первичной и вторичной обмоток; r₁, r₂, L₁₁, L₂₂ – активные сопротивления и собственные индуктивности обмоток; M – взаимная индуктивность обмоток.

Рисунок 1. Схема однофазного двухобмоточного трансформатора

На схеме рисунка 1 указаны положительные направления u и i, причем стрелка u направлена от точки с высшим потенциалом к точке с низшим потенциалом.

При составлении уравнений (1) первичная обмотка рассматривается как приемник, а вторичная – как источник электрической энергии, и сами эти уравнения истолковываются следующим образом.

Первичное напряжение u₁ является приложенным, расходуется на падение напряжения r₁ × i₁ и уравновешивание электродвижущей силы (э. д. с.) первичной обмотки

и состоит поэтому из двух составляющих: r₁ × i₁ и –e₁, что и выражается первым уравнением (1). Вторичное напряжение u₂ возникает вследствие индуктирования во вторичной обмотке э. д. с.

и поэтому

u₂ = e₂ – r₂ × i₂ ,

что соответствует второму уравнению (1). В уравнениях (1) считается, что M > 0 и положительные токи i₁ и i₂ создают в магнитопроводе потоки одинакового направления.

Отметим, что в правой части второго уравнения (1) можно было бы изменить знаки на обратные. Тогда u₂ следовало бы трактовать как напряжение, приложенное к вторичной обмотке со стороны вторичной сети. Некоторые, в особенности иностранные, авторы применяют также и эту последнюю форму записи.

Уравнения напряжения для синусоидально изменяющихся токов и напряжений в комплексной форме

Обычно силовые трансформаторы, а также ряд видов специальных трансформаторов работают с синусоидально изменяющимися токами и напряжениями. В этом случае вместо дифференциальных уравнений (1) удобнее пользоваться комплексными уравнениями для действующих значений токов и напряжений. Для получения этих уравнений в уравнения (1) следует подставить

u₁ = √2 × U₁ × e ^jωt;    u₂ = √2 × U₂ × e ^jωt;
i₁ = √2 × I₁ × e ^jωt;      i₂ = √2 × I₂ × e ^jωt;

и после дифференцирования сократить уравнения на множитель √2 × e ^jωt. Тогда будем иметь

где

представляют собой полные собственные и взаимные индуктивные сопротивления обмоток.

При симметричной нагрузке трехфазных трансформаторов электромагнитные процессы протекают во всех фазах одинаково и соответствующие электромагнитные величины в каждой фазе также одинаковы и лишь сдвинуты по фазе на 120°. Некоторая несимметрия магнитной цепи трехстержневого трансформатора, а также появление в ряде случаев  третьих гармоник потока (смотрите статью "Явления, возникающие при намагничивании магнитопроводов трансформаторов") обычно не оказывают заметного влияния на работу трансформатора под нагрузкой. К тому же эти явления при необходимости можно учесть отдельно. По этим причинам уравнения (2) с большой точностью применимы также для фазных величин трехфазного трансформатора при симметричной его нагрузке. Система уравнений (2) не учитывает лишь потерь в стали магнитопровода трансформатора. Учет этих потерь рассмотрен в отдельных статьях.

Для трехфазного трансформатора в соответствии со сказанным выше U₁, U₂, I₁ и I₂ представляют собой фазные значения напряжений и токов.

Уравнения (1) и (2) полностью определяют процессы, происходящие в трансформаторе при указанных выше допущениях, и позволяют решать задачи, связанные с работой трансформатора. Например, если определить из первого уравнения (2) I₁ и подставить его значение во второе уравнение (2), то получим зависимость вторичного напряжения U₂ от тока нагрузки I₂:

(4)

Первый член правой части выражения (4) определяет величину U₂ = U₂₀ при холостом ходе, то есть при I₂ = 0:

(5)

а второй член – падение напряжения на вторичных зажимах при нагрузке.

Из уравнения (4) можно найти также значение вторичного тока короткого замыкания I₂ = I_2к, когда вторичная обмотка замкнута накоротко и U₂ = 0:

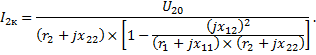(6)

Соображения о точности результатов вычислений на основе представленных уравнений напряжения

Однако на практике расчеты по формулам, получаемым непосредственно из уравнений (1) и (2), и в частности по формулам (4) и (6), не могут быть выполнены с необходимой точностью. Причина этого заключается в том, что входящий в (4) и (6) множитель

представляет собой разность двух весьма близких величин. В этом можно убедиться, если пренебречь весьма малыми по сравнению с x₁₁ и x₂₂ величинами r₁ и r₂. Тогда вместо приведенной выше формы этого множителя получим

(7)

то есть значение коэффициента рассеяния согласно равенству (12), в статье "Индуктивности обмоток трансформатора и электромагнитное рассеяние". Но как уже указывалось выше, определение σ по расчетным или опытным значениям M, L₁₁ и L₂₂ связано с большой погрешностью.

Таким образом, если положить r₁ = r₂ = 0, то вместо (4) и (6) получим соответственно

Из этих соотношений видно, что такие важные с эксплуатационной точки зрения величины, как падение напряжения и ток короткого замыкания, определяются небольшой долей σ полного индуктивного сопротивления x₂₂, обусловленной электромагнитным рассеянием. Это же можно сказать и о ряде других величин, характеризующих эксплуатационные свойства трансформаторов и вращающихся электрических машин. Поэтому определение величин, характеризующих электромагнитное рассеяние, составляет важную задачу теории электрических машин.

Кроме указанных соображений о точности результатов, расчеты на основе уравнений (1) и (2) неудобны также в связи с тем, что ввиду неравенства чисел витков (w₁ ≠ w₂) параметры r₁, r₂, L₁₁, L₂₂, M, x₁₁, x₂₂ и x₁₂, а также напряжения u₁, u₂, U₁, U₂ и токи i₁, i₂, I₁, I₂ могут сильно различаться по значению.

В связи с изложенным теорию электрических машин в отношении рассматриваемых вопросов целесообразно развивать в следующих тесно связанных друг с другом направлениях:
1. Индуктивно связанные обмотки приводятся путем соответствующих пересчетов к одинаковому числу витков, в результате чего порядки напряжений, токов и параметров этих обмоток становятся соответственно одинаковыми.
2. Из полных собственных индуктивностей L₁₁, L₂₂ и индуктивных сопротивлений самоиндукции x₁₁ и x₂₂ выделяются составляющие – индуктивности рассеяния S₁, S₂ и индуктивные сопротивления рассеяния x₁ и x₂, обусловленные явлением электромагнитного рассеяния, причем это выделение производится с таким расчетом, что остающиеся части полных индуктивностей (L₁₁ – S₁, L₂₂ – S₂) и индуктивных сопротивлений (x₁₁ – x₁, x₂₂ – x₂) соответствуют индуктивно связанным цепям с полной связью (c = 1).
3. Разрабатываются непосредственные методы расчета малых параметров – индуктивностей и индуктивных сопротивлений рассеяния – независимо от расчета полных индуктивностей и индуктивных сопротивлений, чем достигается необходимая точность в определении этих малых параметров.
4. От электрических цепей с индуктивной связью делается переход к схемам замещения с электрической связью цепей, что приводит к упрощению расчетов и большей наглядности теории.
5. Индуктивности и индуктивные сопротивления рассеяния вводятся в явном виде в расчетные соотношения и схемы замещения, что позволяет с необходимой точностью рассчитывать величины, зависящие от электромагнитного рассеяния.

Эти вопросы применительно к трансформаторам рассматриваются в следующих статьях.

Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.