Электродвижущая сила якоря
 |
| Рисунок 1. Определение э. д. с. якоря и электромагнитного момента |
Электродвижущую силу якоря (э. д. с. якоря) обозначим буквой N число активных проводников обмотки и рассчитаем э. д. с. якоря Eа в предположении, что y1 = τ и щетки установлены на геометрической нейтрали. Тогда э. д. с. всех N / 2а проводников параллельной ветви складываются арифметически и для вычисления Eа можно просуммировать э. д. с. N / 2p проводников, расположенных под одним полюсом, и умножить результат на 2p / 2a. Таким образом,
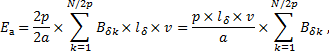 | (1) |
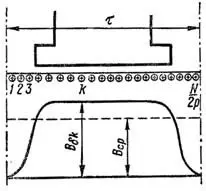
где Bδk – значение индукции под k-м проводником на протяжении полюсного деления (рисунок 1).
При достаточно большом N/2p можно положить (рисунок 1)
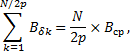
где Bср – среднее значение магнитной индукции на протяжении полюсного деления, равное
Кроме того, окружная скорость якоря
v = 2p × τ × n .
После подстановки этих величин в выражение (1) получим
 | (2) |
или
| Eа = cе × Фδ × n , | (3) |
где
| cе = p × N / a | (4) |
– постоянная для каждой машины величина.
Если вместо величины n ввести в формулу (2) угловую скорость вращения
| Ω = 2 × π × n , | (5) |
то получим
| Eа = cм × Фδ × Ω , | (6) |
где
 | (7) |
Как следует из выражений (3) и (6), э. д. с. Eа пропорциональна основному магнитному потоку и скорости вращения и не зависит от формы кривой распределения индукции в воздушном зазоре.
 |
| Рисунок 2. Определение потока, сцепляющегося с обмоткой при неполном шаге |
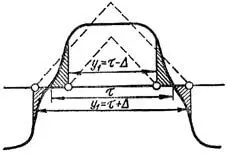
При укороченном или удлиненном шаге обмотки в выражения (2), (3) и (6) вместо Фδ нужно подставлять значение потока, с которым сцепляется секция при симметричном ее расположении относительно полюса (рисунок 2). При этом удлинение шага на некоторую величину Δ равноценно укорочению шага на такую же величину. При наличии скоса пазов нужно исходить из этого же принципа. Однако в обычных условиях, когда удлинение или укорочение шага, а также скос пазов малы, влияние их мало и не учитывается.
Когда щетки сдвинуты с геометрической нейтрали, э. д. с. меньше. При этом в выражения (2), (3) и (6) нужно подставлять значение потока, с которым сцепляется секция в момент ее замыкания накоротко щетками. Если щетки сдвинуты с нейтрали на половину полюсного деления, то Eа = 0.
Электромагнитный момент и электромагнитная мощность
При тех же предположениях, что и при определении Eа, электромагнитный момент машины
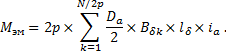
Подставим сюда
Тогда
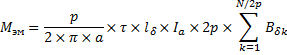
Если выразить сумму в этом выражении, как и выше, через Bср и Фδ, то в окончательной форме получим
| Mэм = cм × Фδ × Iа , | (8) |
причем постоянный для каждой данной машины коэффициент cм определяется равенством (7).
Сделанные выше замечания о влиянии формы кривой поля, шага обмотки, скоса пазов и сдвига щеток с нейтрали действительны и для данного случая. Момент в системе СИ получается в ньютон-метрах (Н × м). При необходимости выразить момент в килограмм-метрах (кгс × м) надо результат разделить на 9,81.
Отметим, что выражение (8) с учетом равенства (7) можно представить также в виде
 | (9) |
откуда следует, что момент пропорционален потоку всех полюсов (2p × Фδ) и току всех проводников якоря 
Из соотношений (6) и (8) вытекают также два равноценных выражения для электромагнитной мощности:
| Pэм = Eа × Iа = Mэм × Ω . | (10) |
При выводе формул э. д. с. и момента предполагалось, что проводники обмотки расположены на гладкой поверхности якоря. В действительности проводники находятся в пазах, где магнитная индукция ослаблена. Однако полученные формулы справедливы и в этом случае, так как э. д. с. и момент определяются значением потока, сцепляющегося с секциями обмотки. При расположении проводников в пазах механические усилия действуют главным образом не на проводники обмотки, а на зубцы якоря.
Источник: Вольдек А.И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.