Расчет магнитной цепи трансформатора

Расчет магнитной цепи производится с целью определения намагничивающего тока и магнитных потерь. Расчет реактивной составляющей намагничивающего тока можно выполнить двумя методами.

Первый метод

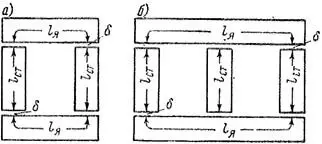
Первый метод аналогичен методу расчета магнитной цепи машины постоянного тока (смотрите статью "Метод расчета магнитной цепи машины постоянного тока"). При этом магнитная цепь вдоль средней магнитной линии (рисунок 1) разбивается на участки (стержни, ярма и воздушные зазоры или щели между ними), в пределах которых магнитные индукции B_ст, B_я, B_δ можно считать постоянными. Задаваясь амплитудой потока стержня Ф_ст, определяют амплитуды индукции B_ст, B_я, B_δ = B_ст и затем по кривым намагничивания стали находят H_ст и H_я. Тогда намагничивающая сила однофазного трансформатора (рисунок 1, а)

(1)

Рисунок 1. Магнитная цепь однофазного (а) и трехфазного стержневого (б) трансформатора

где δ – величина зазора, которая для шихтованных магнитопроводов равна 0,003 – 0,005 см, а для стыковых магнитопроводов больше этого значения на толщину изоляционной прокладки в стыке.

Магнитная цепь трехстержневого трансформатора несколько несимметрична, и длины магнитных линий для крайних фаз несколько больше, чем для средней. Поэтому намагничивающая сила и намагничивающие токи крайних фаз также несколько больше. На практике этим различием пренебрегают и рассчитывают среднюю намагничивающую силу F для одной фазы. Тогда (рисунок 1, б)

(2)

Здесь n_ф – среднее число стыков или зазоров на фазу. Для трехстержневого трансформатора с шихтованным магнитопроводом (смотрите рисунок 2, б) n_ф = 7/3 и со стыковым магнитопроводом n_ф = 2.

Действующее значение основной гармоники реактивной составляющей намагничивающего тока

(3)

где w – число витков обмотки и k – коэффициент, учитывающий наличие в намагничивающем токе высших гармоник. При B_ст = 1 Т и B_ст = 1,4 Т соответственно k = 1,5 и k = 2,2.

Магнитная характеристика Ф_ст = f(i_0r) имеет вид, показанный на рисунке 1, в статье "Явления, возникающие при намагничивании магнитопроводов трансформаторов".

Второй метод

Второй метод основан на вычислении энергии магнитного поля магнитопровода или его намагничивающей (реактивной) мощности.

Допустим, что B и H представляют собой амплитуды индукции и напряженности магнитного поля, изменяющихся синусоидально во времени. Тогда максимум магнитной энергии в единице объема поля

W ’_макс = BH / 2 ,

реактивная мощность на единицу объема

Q ’ = ωW ’_макс = πfBH ,

а реактивная мощность магнитопровода с объемом V или массой G

(4)

где γ – плотность стали магнитопровода, а

(5)

Рисунок 2. Кривые удельной реактивной мощности магнитопровода и зазора

представляет собой реактивную мощность на единицу массы стали магнитопровода.

Для воздушных зазоров выражение для Q можно представить в виде

Q = qnδS_δ = nq_δS_δ ,

где S_δ – площадь зазора; n – число зазоров на весь магнитопровод; q – реактивная мощность на единицу объема зазора; q_δ = qδ – реактивная мощность на единицу площади зазора.

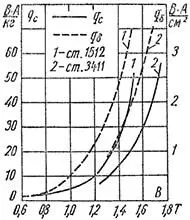
Значение q_с = f(B) в принципе можно вычислить, зная кривую B = f(H) для данного материала. Однако на практике пользуются данными, полученными непосредственно опытным путем. Кривые q_δ = f(B) для шихтованных магнитопроводов также определяются опытным путем, так как в таких магнитопроводах зазоры одного слоя шунтируются листами другого слоя и индукция в зазорах уменьшается, а в листах стали по соседству с зазорами увеличивается, вследствие чего q_δ зависит также от марки стали. Кривые q_с = f(B) и q_δ = f(B) представлены на рисунке 2

Так как реактивная намагничивающая мощность трансформатора

Q₀ = mEI_0r ,

где m – число фаз, то

(6)

Здесь G_ст и G_я – массы стержней и ярем трансформатора, а q_с.ст и q_с.я – удельные мощности q_с для стержня и ярма.

Обычно пользуются вторым методом расчета.

Магнитные потери в магнитопроводе p_мг легко вычислить, зная удельные потери p = f(B) для используемой марки стали:

Активная составляющая намагничивающего тока

(8)

а полный намагничивающий ток, или ток холостого хода,

(9)

Ток I₀ в силовых трансформаторах относительно мал и составляет при нормальном напряжении 0,5 – 4% от номинального тока, причем второе число относится к трансформаторам малой мощности (10 – 20 кВ×А). Малое значение тока I₀ объясняется наличием замкнутого стального магнитопровода.

Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.