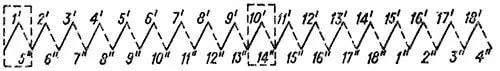Шаги обмотки
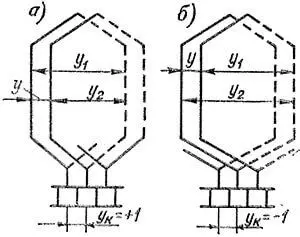
На рисунке 1 представлены два возможных варианта последовательного соединения секций простой петлевой обмотки. Эту обмотку называют также параллельной. На рисунке 1 показаны шаги y1, y2, y рассматриваемой обмотки, которые будем определять по элементарным пазам. Первый частичный шаг y1 вычисляется по формуле (1), в статье "Электродвижущая сила секций", и определяет расстояние по поверхности якоря между начальной и конечной сторонами секции. Второй частичный шаг обмотки y2 определяет расстояние между конечной стороной данной секции и начальной стороной следующей за ней по схеме обмотки секции. Направление движения по якорю и коллектору вправо будем считать положительным. Так как в петлевой обмотке движение при переходе от конечной стороны предыдущей секции к начальной стороне последующей совершается влево, то шаг y2 в петлевой обмотке будем считать отрицательным числом. Результирующий шаг обмотки
| (1) |
определяет расстояние между начальными сторонами данной и следующей за ней секцией.
Рисунок 1. Секции неперекрещенной (а) и перекрещенной (б) простой петлевой обмотки
Коллекторным делением называется ширина коллекторной пластины плюс ширина одной изоляционной прокладки между пластинами. Шаг по коллектору yк определяет расстояние в коллекторных делениях между серединами коллекторных пластин, к которым присоединены концы данной секции или, что то же самое, начала данной и следующей за ней секций. Очевидно,
| (2) |
Соотношения (2), в статье "Электродвижущая сила секций", а также (1) и (2) этой статьи применимы для всех типов обмоток.
Отличительным свойством простой петлевой обмотки является то, что для нее
| (3) |
Знак плюс соответствует случаю |y2| < y1, и такие обмотки называются неперекрещенными (рисунок 1, а). Знак минус соответствует случаю |y2| > y1, и такие обмотки называются перекрещенными (рисунок 1, б). Во втором случае расход меди несколько больше, и поэтому выполнения таких петлевых обмоток избегают. В электромагнитном отношении эти обмотки равноценны и различаются только тем, что при той же полярности полюсов и том же направлении вращения, полярности щеток противоположны.
Схема и основные свойства обмотки
Рассмотрим симметричную простую петлевую обмотку с данными:
![]()
![]()
Рисунок 2. Таблица соединений секционных сторон простой петлевой обмотки, изображенной на рисунке 3
Будем присваивать секционным сторонам номера тех элементарных пазов, в которых они лежат. Тогда по известным значениям шагов можно составить таблицу соединений секционных сторон обмотки (рисунок 2), исходя из определенного элементарного паза и прибавляя к номеру этого паза значение первого частичного шага, значение второго шага, затем опять первого и так далее. Номера верхних сторон секций, изображенных сплошными линиями, проставлены в таблице на рисунке 2 сверху, а номера нижних сторон секций, изображенных штриховыми линиями, – снизу. От нижней секционной стороны 4” (справа на рисунке 2) по ходу обмотки вернемся опять к верхней стороне 1’, так как 4 + y2 = 4 – 3 = 1. Таким образом, обмотка является замкнутой.
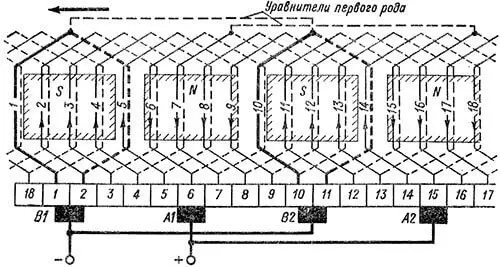
По известным шагам или таблице соединений секционных сторон можно начертить также схему обмотки (рисунок 3).
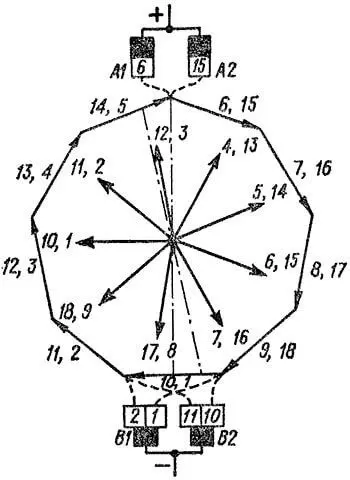
Рисунок 3. Схема простой петлевой обмотки с 2×p = 4, Z = Zэ = S = K = 18, y1 = 4, y2 = –3, y = yк = +1
На рисунке 3 проставлены номера элементарных пазов. Условимся, как это сделано на рисунке 3, присваивать коллекторной пластине номер той секции, с началом которой соединена эта пластина.
Линия на поверхности якоря, проходящая в осевом направлении посередине между двумя соседними полюсами, называется линией геометрической нейтрали или геометрической нейтралью, так как вдоль этой линии магнитная индукция B = 0 (смотрите рисунок 2, в статье "Электродвижущая сила секций").
При вращении якоря некоторая часть секций, выделенных на рисунке 3 жирными линиями, оказывается неизбежно замкнутой накоротко через щетки. Чтобы индуктируемые в этих секциях электродвижущие силы были минимальны и в секциях не возникало чрезмерных токов, которые вызовут перегрузку щеточных контактов, такие короткозамкнутые секции должны находиться на линии геометрической нейтрали или в ближайшей от этой линии нейтральной зоне. Для этого щетки устанавливают так, чтобы в середине периода короткого замыкания стороны секции располагались симметрично относительно середины полюса. Тогда говорят, что щетки установлены на нейтрали. При симметричной форме лобовых частей секций щетки расположены по осям полюсов (рисунок 3).
Совершим обход цепи обмотки (рисунок 3) слева направо, начиная с секции 2. Проходя последовательно, начиная от щетки В1, секции 2, 3, 4 и 5, мы мысленно движемся по направлению индуктируемых электродвижущих сил и выходим к щетке А1. Следовательно, эти секции составляют одну параллельную ветвь, электродвижущая сила которой равна сумме электродвижущих сил этих секций. Проходя затем от щетки А1 к щетке В2 по контуру секций 6, 7, 8, 9, мы обойдем вторую параллельную ветвь, двигаясь против направления индуктируемых электродвижущих сил. Секция 10 замкнута накоротко. Секции 11, 12, 13 и 14, расположенные между щетками В2 и А2, составляют третью ветвь, а секции 15, 16, 17 и 18, расположенные между щетками А2 и В1, – четвертую ветвь. Обход этой последней ветви также совершается против направления электродвижущей силы, причем после нее мы приходим к пластине 1. Секция 1 также замкнута накоротко. Через каждую щетку простой петлевой обмотки протекают токи двух параллельных ветвей.
Верхние стороны секций каждой параллельной ветви находятся под одним полюсом, а нижние – под другим. На рисунке 2 короткозамкнутые секции обведены штриховыми прямоугольниками.
Таким образом, обмотка на рисунке 3 имеет четыре параллельные ветви, а в общем случае простая петлевая обмотка содержит
| (4) |
параллельных ветвей, что является характерной особенностью этой обмотки. Очевидно, что условия симметрии, описанные в соотношениях (5), (6) и (7), в статье "Общие сведения о якорных обмотках машин постоянного тока", для обмотки, изображенной на рисунке 3, удовлетворяются.
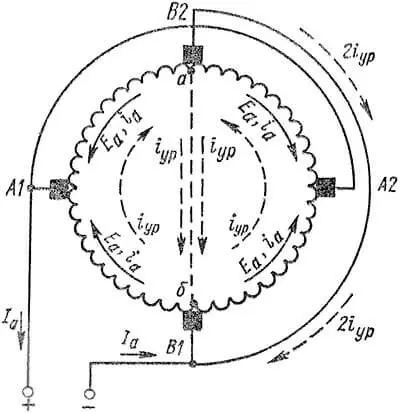
Если машина работает в режиме генератора, стрелки на рисунке 3 указывают также направление токов в обмотке. При этом полный ток якоря Iа тоже распределяется по четырем ветвям. В соответствии с изложенным цепь обмотки (рисунок 3) можно изобразить упрощенно, как показано на рисунке 4, где ветви обмотки и распределение тока выглядит более наглядно.
Рисунок 4. Упрощенное представление цепи обмотки, показанной на рисунке 3
На основании рассмотрения рисунка 3 можно установить также следующее. Если обмотка имеет полный шаг и щетки установлены на нейтрали, то электродвижущая сила ветви будет наибольшей. Кроме того, при этом направления токов всех проводников, лежащих под одним полюсом, будут одинаковы, и поэтому развиваемый электромагнитный момент будет максимальным. Следовательно, такое устройство обмотки и такое расположение щеток являются наиболее выгодными. Небольшое отклонение шага y1 от полного не оказывает заметного влияния на значения электродвижущей силы и вращающего момента, так как изменение направлений электродвижущих сил и токов при этом происходит только в таких проводниках параллельной ветви, которые располагаются вблизи нейтрали, то есть в зоне слабого магнитного поля.
Расположение параллельных ветвей в пространстве относительно неподвижных полюсов определяется положением щеток и также неизменно. При вращении якоря секции переходят попеременно из одной ветви в другую, причем во время такого перехода секция замыкается накоротко щеткой и в ней происходит изменение направление тока, например от значения +iа до значения –iа. Это явление называется коммутацией секции. Явления в короткозамкнутой секции влияют, как уже указывалось, на значения токов в щеточном контакте и на работу щеток. Совокупность явлений, связанных с замыканием секций накоротко щетками, переходом этих секций из одних параллельных ветвей обмотки в другие и передачей тока через скользящий контакт между коллектором и щеткой, называется коммутацией машины. Подобно вопросы коммутации рассматриваются в статье "Процесс коммутации".
Векторная диаграмма электродвижущих сил обмотки
Пользуясь рассмотренной в статье "Электродвижущая сила секций" звездой электродвижущих сил секций, можно построить векторную диаграмму электродвижущих сил обмотки, складывая векторы электродвижущих сил секций в той последовательности, в какой секции соединены по контуру обмотки.
Такая диаграмма вместе со звездой электродвижущих сил секций для обмотки, показанной на рисунке 3, изображена на рисунке 5. Поскольку векторы электродвижущих сил соседних секций при Z = 18 и 2 × p = 4 сдвинуты на 40° (смотрите статью "Электродвижущая сила секций"), то после построения векторов девяти секций происходит поворот на 9 × 40° = 360° и многоугольник электродвижущих сил замыкается. После обхода остальных девяти секций получается второй многоугольник, накладывающийся на первый.
Каждый многоугольник электродвижущих сил соответствует одной паре параллельных ветвей. В общем случае при простой петлевой обмотке получается p многоугольников, которые при полной идентичности всех пар параллельных ветвей накладываются друг на друга, что свидетельствует о симметрии обмотки.
Начала векторов 1, 2, 3 … на рисунке 5 представляют собой потенциалы начал секций 1, 2, 3 … , а также потенциалы коллекторных пластин 1, 2, 3 … Совпадение концов и начал векторов обоих многоугольников на рисунке 5 указывает на наличие в обмотке равнопотенциальных точек. Например, равные потенциалы имеют коллекторные пластины 1 и 10, 2 и 11 и так далее, то есть вообще пластины, удаленные друг от друга на
| (5) |
коллекторных делений. Такой вывод для симметричной обмотки вполне естественен, так как стороны секций, сдвинутых на yп элементарных пазов, находятся под полюсами одинаковой полярности, в одинаковом магнитном поле. Величина yп называется потенциальным шагом.
На диаграмме электродвижущих сил можно показать условно также щетки, как это сделано на рисунке 5 для положения обмотки относительно щеток согласно рисунку 3. Многоугольник электродвижущих сил надо представлять себе вращающимся, и сумма проекций векторов одной ветви или одной половины многоугольника на вертикальную ось щеток будет равна электродвижущей силе ветви и обмотки в целом. Значение этой электродвижущей силы пульсирует между значениями, которые соответствуют длинам двух штрих-пунктирных линий на рисунке 5. Можно показать, что уже при K / 2×p = 10 эти пульсации составляют менее 1%. В действительности эти пульсации еще меньше вследствие того, что вблизи геометрической нейтрали индукция поля полюсов значительно меньше его основной гармоники.
Уравнительные соединения
В идеальных условиях, когда обмотка симметрична и потоки всех полюсов равны, электродвижущие силы всех ветвей также равны и ветви нагружаются токами равномерно. Однако в действительности из-за производственных и иных отклонений (неодинаковый воздушный зазор под разными полюсами, неоднородность материалов сердечников и тому подобного) потоки отдельных полюсов не будут в точности равны. При этом электродвижущие силы ветвей простой петлевой обмотки также не будут равны, так как ветви сдвинуты относительно друг друга на одно полюсное деление (рисунок 3).
Предположим, что на рисунке 4 электродвижущие силы нижних ветвей больше, чем электродвижущие силы верхних ветвей. При этом уже при холостом ходе генератора, когда Iа = iа = 0, внутри обмотки будут циркулировать уравнительные токи iур, которые замыкаются через щетки одинаковой полярности и соединительные провода или шины между ними. Так как внутреннее сопротивление обмотки мало, то эти токи могут быть значительными уже при небольшой разнице в потоках отдельных полюсов. При работе машины токи нагрузки щеток 2 × iа будут алгебраически складываться с токами 2 × iур, в результате чего щетки В1, В2 окажутся перегруженными, а щетки А1, А2 – недогруженными. Правильная работа щеток при этом может нарушиться. Еще более серьезное влияние на условия работы щеток оказывает нарушение баланса электродвижущих сил в короткозамкнутых секциях, вызванное уравнительными токами.
Для того чтобы разгрузить щетки от уравнительных токов и дать этим токам возможность замкнуться внутри самой обмотки, обмотка снабжается уравнительными соединениями, или уравнителями. Уравнители соединяют внутри обмотки точки, которые теоретически имеют равные потенциалы.
Как было установлено выше, эти точки сдвинуты на пару полюсов или при 2×p = 4 на половину окружности якоря или коллектора. Одно уравнительное соединение показано на рисунке 4 штриховой линией аб по вертикальному диаметру. Так как сопротивление щеточных контактов значительно больше сопротивления уравнительного провода, то токи iур замыкаются по этому проводу, минуя щетки, как показано на рисунке 4. Такие соединения, применяемые в простых петлевых обмотках, называются уравнителями первого рода.
На векторных диаграммах при наличии равнопотенциальных точек концы или начала векторов соответствующих секций совпадают.
Уравнители выполняются либо на стороне коллектора (и тогда они соединяют пластины с равными потенциалами), либо на противоположной от коллектора стороне (и тогда они соединяют равнопотенциальные точки лобовых частей секций). Шаг уравнителей yур равен потенциальному шагу обмотки yп:
| (6) |
При равенстве потоков полюсов токи в уравнителях не возникают. На рисунке 3 штриховыми линиями показаны два уравнителя первого рода.
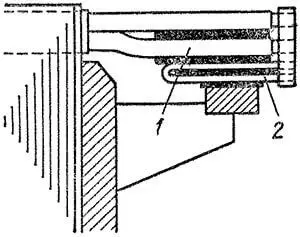 |
| Рисунок 6. Уравнители (2), размещенные под лобовыми частями (1) на стороне якоря, противоположной коллектору |
Для достижения надлежащего эффекта при всех положениях вращающегося якоря обмотку нужно снабдить достаточным числом уравнителей. Из рассмотрения многоугольника электродвижущих сил (рисунок 5) видно, что максимальное число возможных уравнителей первого рода на одной стороне якоря равно K/p, причем каждый из них соединяет p точек равного потенциала. Полным количеством уравнителей снабжаются только крупные машины с тяжелыми условиями коммутации тока. В остальных случаях выполняют от 1/3 до 1/6 всех возможных уравнителей или один уравнитель на один-два паза машины. При этом их размещают равномерно по окружности якоря. Сечение уравнителей берут равным 20 – 50% сечения витка обмотки якоря. На рисунке 6 показан один из вариантов конструктивного выполнения уравнителей.
Протекающие по обмотке уравнительные токи являются переменными, и по правилу Ленца они создают магнитное поле, которое стремиться устранить неравенство потоков полюсов. Поэтому наличие уравнителей приводит также к значительному ослаблению уравнительных токов.
Простые петлевые обмотки с uп > 1
Обмотка на рисунке 3 имела 2 × p = 4, Z = Zэ = S = K =18 и uп = 1. Рассмотрим теперь обмотку при тех же 2 × p = 4 и Z = 18, но uп = 2 и Zэ = S = K = 36. Если при этом сохраним шаг по пазам y1z = 4, то y1 = uп × y1z = 2 × 4 = 8, y2 = –7, y = yк = +1. Эта обмотка будет равносекционной.
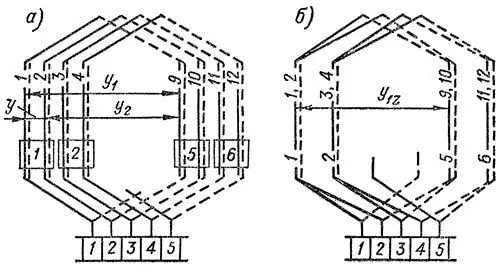
Схему такой обмотки можно изображать двояким образом, как показано на рисунке 7, а и б. Верхний ряд цифр на этом рисунке представляет собой номера секций, а нижний ряд – номера пазов.
Рисунок 7. Варианты изображения равносекционной обмотки с 2 × p = 4, Z = 18, uп = 2, Zэ = S = K = 36, y1 = 8, y2 = –7, y = yк = +1
Так как число пазов не изменилось, то и звезда пазовых электродвижущих сил не изменится (смотрите рисунок 2, б, в статье "Электродвижущие силы секций"). Векторы электродвижущих сил каждой пары секций (1 – 2, 3 – 4 и так далее) будут совпадать по фазе, а векторы электродвижущих сил секций, лежащих в соседних пазах (секции 2 – 3, 4 – 5 и так далее), будут сдвинуты на 40°, как и в предыдущем случае. Поэтому многоугольник электродвижущих сил обмотки будет выглядеть так же, как и на рисунке 5, с тем лишь различием, что каждая сторона многоугольника будет представлять собой сумму электродвижущих сил двух секций, лежащих в общих пазах.
Если при тех же значениях 2 × p, Z и Zэ выбрать шаги по элементарным пазам
y1 = 36 / 4 = 9; y2 = 1 – 9 = –8,
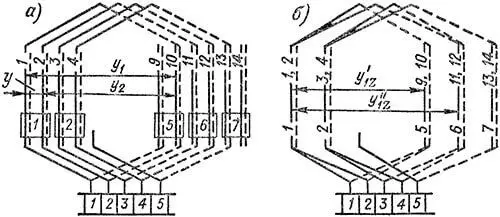
то обмотка будет ступенчатой. Схема такой обмотки также может быть изображена двояким образом, как показано на рисунке 8, а и б. При этом обмотка имеет два значения шага y1z по зубцам; y’1z = 4 и y’1z = 5.
Рисунок 8. Варианты изображения ступенчатой обмотки с 2 × p = 4, Z = 18, uп = 2, Zэ = S = K = 36, y1 = 9, y2 = –8, y = yк = +1
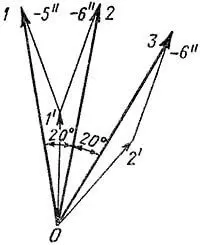
Построим векторы электродвижущих сил секций 1, 2, 3 этой обмотки (рисунок 9). Секция 1 лежит в пазах 1 и 5, и ее электродвижущая сила равна разности векторов 1 и 5 звезды на рисунке 2, б, в статье "Электродвижущие силы секций". Построенный таким образом вектор секции 1 на рисунке 9 обозначен 1, а составляющие его векторы пазов или секционных сторон обозначены 1’ и – 5”. Секция 2 лежит в пазах 1 и 6, а секция 3 – в пазах 2 и 6, и векторы электродвижущих сил этих секций построены и обозначены на рисунке 9 по такому же принципу, как и вектор секции 1. Как следует из этого рисунка, векторы электродвижущих сил секций сдвинуты относительно друг друга на 20°, то есть на половину угла, соответствующего пазовому делению. Таким образом, ступенчатая обмотка с Z = 18 и Zэ = 36 в этом отношении равноценна обмотке с удвоенным числом пазов Z = Zэ = 36. Соответственно этому многоугольник электродвижущих сил ступенчатой обмотки будет иметь в два раза больше сторон и в большей мере приближаться к окружности, чем при равносекционной обмотке. Это является некоторым преимуществом ступенчатой обмотки. Однако главное преимущество такой обмотки состоит в улучшении условий коммутации.
Уравнители первого рода для рассмотренных равносекционной и ступенчатой обмоток выполняются также просто, как и в ранее рассмотренном случае. Разница заключается лишь в том, что вследствие удвоения S = K шаг уравнителей yур также удваивается.
Аналогично схемам на рисунках 7 и 8 можно изображать также схемы и других типов обмоток при uп > 1.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.