Метод наложения токов

Метод наложения применяется для расчета электрических цепей, имеющих несколько источников электродвижущих сил (ЭДС). Сущность метода наложения состоит в том, что ток в какой либо части цепи можно считать состоящим из ряда частичных токов, вызванных каждой отдельной ЭДС, причем остальные ЭДС принимаются равными нулю.

Рассмотрим пример метода наложения.

Пример 1 (рисунок 1, а). Дано E₁ = 27 В, E₂ = 24 В, r₁ = 3 Ом, r₂ = 4 Ом, r₃ = 6 Ом. Определить, как распределяются токи в цепи.

Произведем расчет методом наложения. Найдем токи, созданные электродвижущей силой E₁ (электродвижущая сила E₂ принята равной нулю) (рисунок 1, б). Выберем положительные направления токов, определим сопротивление участков цепи и токи на каждом участке. Сопротивление r₂ и r₃ соединены параллельно. Поэтому сопротивление разветвления:

Полное сопротивление цепи:

r = r₁ + r_2,3 = 3 + 2,4 = 5,4 Ом .

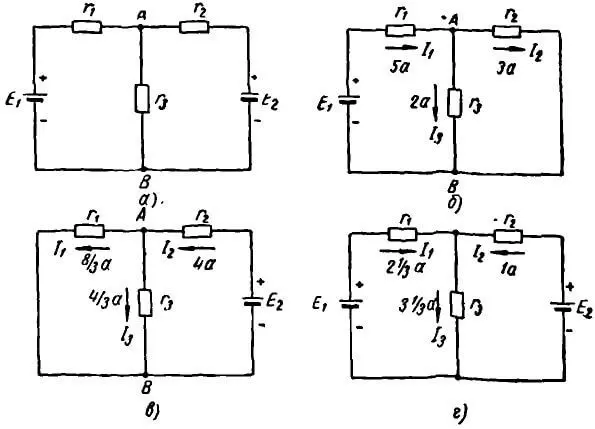
Рисунок 1. Расчет цепи методом наложения – к примеру 1

Ток на общем участке цепи:

Напряжение между точками А и В.

U_АВ = E₁ – I₁ × r₁ = 27 – 5 × 3 = 12 В.

Токи в параллельных ветвях:

Проверка.

I₂ + I₃ = 3 + 2 = 5 А = I₁ .

Найдем токи, созданные ЭДС E₂ (ЭДС E₁ принята равной нулю) (рисунок 1, в). Выберем положительные направления токов, определим сопротивления участков цепи и токи на каждом участке.

r = r₂ + r₁,3 = 4 + 2 = 6 Ом .

UА,В = E₂ – I₂ × r₂ = 24 – 4 × 4 = 8 В.

Проверка.

Сравнивая две последние схемы (рисунок 1, б и в), видим, что на каждом участке (в каждой ветви) цепи протекают два тока. Проведя алгебраическое сложение этих токов (таблица 1), получим действительный ток данного участка.

Таблица 1

Проверка.

По первому закону Кирхгофа для точки А имеем:

Токораспределение по схеме, представленной на рисунке 1, а, дано на рисунке 1, г.

Таким образом производится решение задач методом наложения.

Источник: Кузнецов М.И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560с.