Метод контурных токов применяется для расчета сложных электрических цепей, имеющих больше двух узловых точек. На рисунке 1, а изображена такая электрическая цепь. В ней три контура, причем средний контур имеет участки, входящие в состав двух соседних контуров, которые входят в состав одного контура.
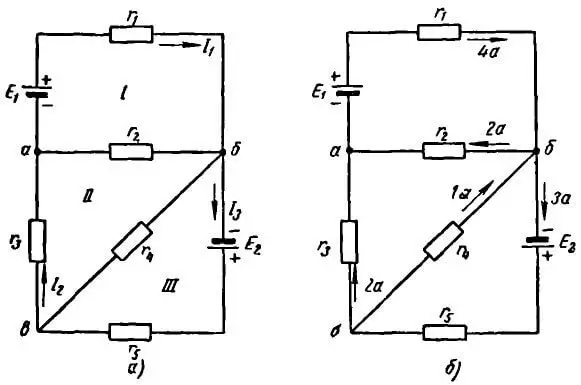
Рисунок 1. Метод контурных токов пример
Сущность метода контурных токов заключается в предположении, что в каждом контуре проходит свой ток (контурный ток). Тогда на общих участках, расположенных на границе соседних контуров, будет протекать ток, равный алгебраической сумме токов этих контуров.
Выберем положительные направления трех контурных токов так, как указано на чертеже стрелками. Затем составим уравнения по второму закону Кирхгофа, обходя все три контура в одном направлении, например в направлении движения часовой стрелки.
Для контура I:
| E1 = I1 × r1 + (I1 – I2) × r2 . | (а) |
Для контура II:
| 0 = I2 × r3 + (I2 – I1) × r2 + (I2 – I3) × r4 . | (б) |
Для контура III:
| E2 = I3 × r5 + (I3 – I2) × r4 . | (в) |
Как мы видим, число уравнений равно числу контуров, то есть число уравнений меньше, чем при решении задачи по законам Кирхгофа. Решая систему уравнений, находим контурные токи, по которым определяются токи в ветвях. Пример решения задач методом контурных токов показан ниже.
Пример 1. Определить, как распределяются токи в цепи, представленной на рисунке 1, а, если E1 = 14 В, E2 = 20 В, r1 = 2 Ом, r2 = 3 Ом, r3 = 4 Ом, r4 = 2 Ом, r5 = 6 Ом. Произведем расчет методом контурных токов.
Решение.
Уравнение для контура I по формуле (а):
14 = I1 × 2 + (I1 – I2) × 3 ,
14 = 2I1 + 3I1 – 3I2 ,
| 14 = 5I1 – 3I2 . | (а') |
Уравнение для контура II по формуле (б):
0 = I2 × 4 + (I2 – I1) × 3 + (I2 – I3) × 2 ,
0 = 4I2 + 3I2 – 3I1 + 2I2 – 2I3 ,
| 0 = 9I2 – 3I1 – 2I3 . | (б') |
Уравнение для контура III, по формуле (в):
20 = I3 × 6 + (I3 – I2) × 2 ,
20 = 6I3 + 2I3 – 2I2 ,
20 = 8I3 – 2I2 ,
| 10 = 4I3 – I2 . | (в') |
Складывая выражения (а’) и (б’), получим:
![]()
или
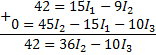
Складывая выражения (в’) и (г), получим:
![]()
или
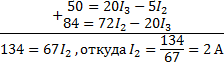
Подставляя значение тока I2 в уравнение (в’), получим:
10 = 4I3 – 2 ,
10 + 2 = 4I3 ,
откуда
![]()
Подставляя значение тока I2 в уравнение (а’), получим:
14 – 5I1 – 6 ,
20 = 5I1 ,
откуда
![]()
Таким образом, все контурные токи найдены.
Определяем на отдельных участках цепи алгебраически, складывая протекающие по ним токи. Токораспределение на отдельных участках цепи показано на рисунке 1, б.
Источник: Кузнецов М. И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560с.