В статье рассказывается как в воздушном зазоре, между полюсом и якорем, можно рассчитать индукцию и намагничивающую силу, как при этом учесть влияние пазов и вентиляционных каналов.
Гладкий якорь
Наиболее сложный характер имеет магнитное поле в воздушном зазоре, на который приходится наибольшая часть полной намагничивающей силы (до 60 – 80%).
Предположим сначала, что пазы на поверхности якоря и радиальные вентиляционные каналы отсутствуют.
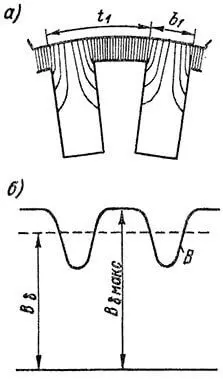
На рисунке 1, а показан характер магнитного поля в зазоре вдоль окружности якоря, а на рисунке 1, б – кривая 1 распределения магнитной индукции Bδ на поверхности гладкого якоря на протяжении полюсного деления
![]()
где Dа – внешний диаметр якоря и 2×p – число полюсов.
Для расчетных цепей кривую 1 заменяют прямоугольником 2 (штриховая кривая на рисунке 1, б) шириной Bδ и высотой, равной действительному значению индукции Bδ в средней части зазора. Площадь прямоугольника равна площади фигуры, ограниченной кривой 1 и осью абсцисс, что означает равенство потоков, соответствующих кривым 1 и 2.
Величина Bδ называется расчетной полюсной дугой, она отличается от реальной полюсной дуги bn (рисунок 1, а) на некоторое значение, зависящее от формы полюсного наконечника. Точное значение Bδ может быть установлено путем построения картины поля в зазоре графическим методом или путем расчета методом конформных отображений. Однако применение этих методов ввиду их большой трудоемкости каждый раз затруднительно, и поэтому пользуются приближенными соотношениями, установленными соответствующими расчетами для разных очертаний полюсных наконечников. При очертании наконечника, показанном на рисунке 1, а,
Bδ = bn ,
а при равномерном зазоре δ по всей ширине наконечника
Bδ = bn + 2 × δ .
Величина
αδ = Bδ / τ
 |  |
| Рисунок 1. Распределение магнитной индукции в воздушном зазоре при гладком якоре | Рисунок 2. Магнитное поле у края сердечника якоря |
называется расчетным коэффициентом полюсной дуги. Для машин с дополнительными полюсами αδ = 0,60 – 0,75 и для машин без дополнительных полюсов αδ = 0,70 – 0,85.
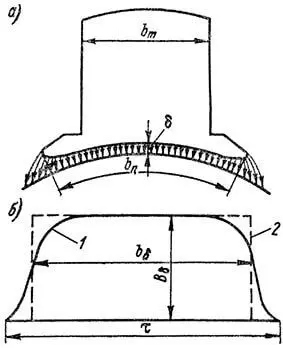
Длину якоря в осевом направлении lа часто принимают на 5 – 10 мм больше длины полюсов lm (рисунок 2, а). При этом индукция на конце якоря ослабляется (рисунок 2, б) и поток, входящий в торец якоря, уменьшается. В результате уменьшаются потери на вихревые токи в нажимных фланцах и в сердечнике якоря от торцевого потока. Расчетная длина якоря в данном случае принимается равной
| (1) |
Таким образом, индукция в воздушном зазоре
| (2) |
и намагничивающая сила воздушного зазора при гладком якоре
| (3) |
Учет влияния пазов и вентиляционных каналов
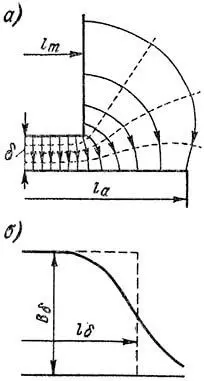
При наличии на якоре пазов поле над ними ослабляется (рисунок 3, а) и кривая Bδ вдоль зазора принимает зубчатый вид (рисунок 3, б). Формула (2) дает значение средней индукции в зазоре Bδ, в то время как в выражение (3) необходимо подставить теперь значение индукции против центра зубца Bδ макс.
Рисунок 3. Магнитное поле в воздушном зазоре при зубчатом якоре
Отношение
kδ1 = Bδ макс / Bδ
называется коэффициентом воздушного зазора, обусловленным зубчатостью якоря. Значение устанавливается на основе анализа поля в зазорах и пазах методом конформных отображений. Однако получаемые при этом соотношения весьма сложные, и на практике пользуются приближенным выражением
| (4) |
где
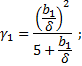 | (5) |
b1 – ширина открытия паза у поверхности воздушного зазора; t1 = π × Dа / Z – величина зубцового деления; Z – число зубцов якоря.
Вместо выражения(4) иногда пользуются также более приближенными соотношениями. Обычно kδ1 = 1,10 – 1,35.
Подставив в формулу (3) вместо Bδ значение Bδ макс = kδ1 × Bδ, получим
| (6) |
Иногда пазы делают также в полюсных наконечниках, и в них размещается так называемая компенсационная обмотка. В этом случае по формулам вида (4) и (5) рассчитывается также коэффициент зазора для полюсов kδ2, причем вместо t1 и b1 подставляется зубцовый шаг t2 и величина открытия паза b2 компенсационной обмотки.
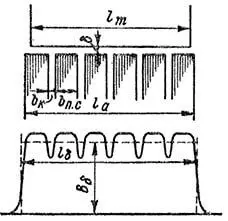
При наличии радиальных вентиляционных каналов кривая поля вдоль зазора в осевом направлении также приобретает зубчатый характер (рисунок 4). При этом рассчитывается коэффициент зазора
| (7) |
где
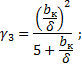 | (8) |
bп.с – ширина пакета стали и bк – ширина вентиляционного канала.
Заметим, что иногда влияние радиальных вентиляционных каналов учитывают более приближенно, принимая в выражении (1) lа равным не полной длине сердечника якоря (рисунок 4), а суммарной ширине пакетов плюс половина суммарной ширины каналов. Коэффициент kδ3 при этом рассчитывать не надо. Отметим, что расчетное значение Bδ при этом будет несколько больше.
Рисунок 4. Магнитное поле в воздушном зазоре в осевом направлении
Учет влияния бандажных канавок
Когда обмотка якоря в пределах сердечника укрепляется бандажами, неравномерность зазора вызывается также канавками под эти бандажи. Однако учет этой неравномерности дополнительным коэффициентом зазора вида (4) не оправдан, так как этот коэффициент получен в предположении, что пазы и вентиляционные каналы глубоки, в то время как бандажные канавки не глубоки. Расчетные соотношения в этом случае можно получить следующим образом.

Рисунок 5. Якорь с бандажными канавками
Если зазор в осевом направлении имеет ступенчатую форму (рисунок 5), то относительная магнитная проводимость зазора на единицу длины дуги по окружности якоря
λ12 = l1 / δ1 + l2 / δ2 ,
а в случае, когда δ2 = δ1,
![]()
Отношение
![]()
определяет коэффициент уменьшения проводимости или увеличения эквивалентного зазора в результате наличия ступени с увеличенным зазором δ2. На основе этого соотношения коэффициент увеличения эквивалентного зазора под влиянием бандажей из немагнитного материала
| (9) |
где nб – число бандажных канавок; bб – ширина бандажной канавки; hб – глубина бандажной канавки.
Когда бандажи изготовлены из магнитного материала, сечение бандажных канавок nб × bб × hб нужно уменьшить на общее сечение бандажных проволок или принять kδ4 приближенно равным единице.
Заключение
Общий коэффициент воздушного зазора, как показывает анализ этого вопроса, можно рассчитать в виде произведения частичных коэффициентов зазора:
| (10) |
тогда вместо выражения (6) имеем
| (11) |
При этом Bδ по-прежнему определяется равенством (2). Величину
δ’ = kδ × δ
в выражении (11) можно назвать эквивалентным воздушным зазором. Значение kδ [смотрите формулу (10)] в машинах постоянного тока изменяется в пределах kδ = 1,1 – 1,8.
В расчетной практике часто Bδ выражают в гауссах (Bδ Гс), а δ – в сантиметрах (δ см). Переходя в выражение (11) от единиц СИ к указанным единицам, получаем
| (12) |
В некоторых случаях рассчитывают также намагничивающую силу на небольшой зазор (0,01 – 0,03 см) между полюсами и ярмом, который неизбежно возникает по технологическим причинам.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.