Индуктивности обмоток
В трансформаторах со стальным магнитопроводом магнитная проницаемость стали µ во время цикла перемагничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные L и взаимные М индуктивности обмоток трансформатора. В результате такого непостоянства µ при подключении трансформатора к сети с синусоидальным напряжем в его намагничивающем токе i0 возникают высшие гармоники (смотрите статью "Явления, возникающие при намагничивании магнитопроводов трансформаторов").
При работе трансформатора на ток i0 накладывается ток нагрузки, по отношению к которому ток i0 и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока i0. Это равносильно допущению, что во время цикла перемагничивания µ, L и M постоянны. Влияние насыщения магнитопровода при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока магнитопровода, значения µ, L и M для данного режима работы. В соответствии с изложенным будем полагать, что µ, L и M постоянны.
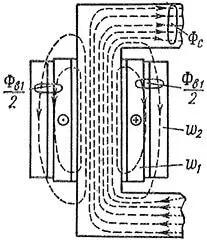
Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком магнитопровода Фс, все силовые линии которого полностью замыкаются по замкнутому магнитопроводу и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рисунок 1).
Пусть поток Фс создается током первичной обмотки i1, когда ток вторичной обмотки i2 = 0. Значения Фс и i1 могут быть известны, например, из данных расчета магнитной цепи или из опыта. Тогда собственная индуктивность первичной обмотки от потока в магнитопроводе
| Lс1 = w1 × Фс / i1. | (1) |
Величину Lс1 можно выразить также через магнитное сопротивление магнитопровода
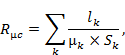 | (2) |
где lk, Sk и µk соответственно означают длину, площадь сечения и магнитную проницаемость k-го участка магнитной цепи. При этом
| Фc = F1 / Rµc = w1× i1 / Rµc. | (3) |
и после подстановки этого значения Фс в выражение (1) получим
| Lc1 = w1² / Rµс | (4) |
Отметим, что значение Rµc также может быть определено по данным расчета магнитной цепи или из данных опыта по соотношению (3).
Аналогично индуктивность вторичной обмотки от потока магнитопровода
| Lc2 = w2² / Rµс | (5) |
а взаимная индуктивность первичной и вторичной обмоток от потока магнитопровода
| Mс = w1 × w2 / Rµс | (6) |
Картина магнитного поля, замыкающегося целиком по магнитопроводу, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление потоку Фс одинаково для поля обеих обмоток и в равенства (4), (5) и (6) входит одинаковая величина Rµс. Вследствие этого также
| (7) |
Кроме потока Фс, ток первичной обмотки i1 создает также поток Фв1 (рисунок 1), силовые линии которого замыкаются частично по воздуху или через трансформаторное масло. Потокосцеплениям Ψв1 и Ψв12 этого потока с первичной и вторичной обмотками соответствует собственная индуктивность первичной обмотки
Lв1 = Ψв1 / i1
и взаимная индуктивность двух обмоток
Mв12 = Ψв12 / i1.
Точно так же при питании вторичной обмотки током i2 создается поток Фв2, замыкающийся частично по воздуху. Потокосцеплениям Ψв2 и Ψв21 этого потока с вторичной и первичной обмотками соответствует собственная индуктивность вторичной обмотки
Lв2 = Ψв2 / i2
и взаимная индуктивность двух обмоток
Mв21 = Ψв21 / i2.
При этом, согласно принципу взаимности,
Mв12 = Mв21 = Mв
Поля потоков Фв1 и Фв2 имеют гораздо более сложный характер, чем поле потока Фс. Отдельные магнитные линии этих потоков сцепляются с неполными и разными числами витков первичной и вторичной обмоток. Поэтому в отличие от Lс2 [смотрите соотношение (7)]
| (8) |
Полные собственные индуктивности первичной и вторичной обмоток
| L11 = Lс1 + Lв1; L22 = Lс2 + Lв2, | (9) |
и полная взаимная индуктивность
| M = Mс + Mв. | (10) |
Первые слагаемые равенств (9) и (10) значительно больше вторых, так как потоки через воздух относительно малы.
Понятие об электромагнитном рассеянии
Полнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей
| (11) |
Как известно из курса теоретических основ электротехники, в реальных условиях всегда c < 1.
Если бы в трансформаторе отсутствовали потоки Фв1 и Фв2, замыкающиеся по воздуху, то L11 = Lc1, L22 = Lc2, M = Mc, и в этом случае в соответствии с равенствами (4), (5), (6) и (11)
![]()
Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством c < 1, обусловлена наличием потоков Фв1 и Фв2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие c = 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки, что фактически невозможно.
Явление неполной электромагнитной связи называется электромагнитным рассеянием.
Наряду с соотношением (11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния
| (12) |
Чем меньше c и чем больше σ, тем больше рассеяние.
Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Фв1 и Фв2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Фв1 и Фв2 обусловливают также явление взаимной индукции, поскольку Mв ≠ 0. Степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие технические показатели и характеристики трансформаторов и вращающихся электрических машин.
В трансформаторах с ферромагнитным магнитопроводом потоки Фв1 и Фв2 относительно малы.
Поэтому электромагнитная связь в трансформаторах чрезвычайно высока, а рассеяние мало.
В силовых трансформаторах, например, c = 0,998 – 0,9995 и соответственно σ = 0,001 – 0,004.
Вследствие этого значение σ, определяемое по формуле (12), представляет собой разность весьма близких величин и вычисление σ по этой формуле связано с очень большими погрешностями, так как L11, L22 и M в практических устройствах не могут быть рассчитаны или определены из опыта с достаточной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.