Пусть имеется однородное магнитное поле, образованное между полюсами NS электромагнита (рисунок 1, а).
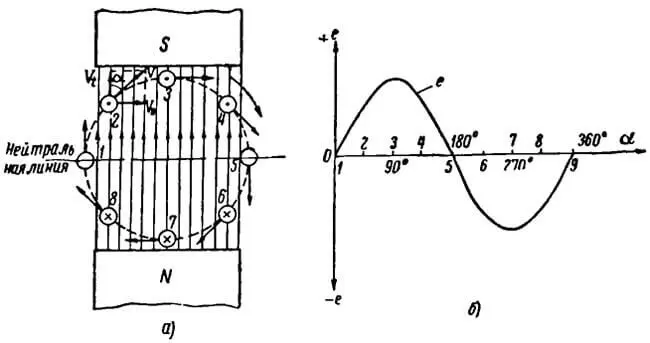
Рисунок 1. Принцип получения переменного тока
а – вращение проводника в однородном магнитном поле; б – график изменения переменного тока
Внутри поля под действием посторонней силы вращается по окружности в сторону движения часовой стрелки металлический прямолинейный проводник. Как известно, пересечение проводником магнитных линий приведет к появлению в проводнике индуктированной электродвижущей силы (ЭДС). Величина этой ЭДС, как было указано в статье "Величина и направление ЭДС индукции", зависит от величины магнитной индукции B, активной длины проводника l, скорости пересечения проводником магнитных линий v и синуса угла α между направлением движения проводника и направлением магнитного поля.
e = B × l × v × sin α .
Разложим окружную скорость v на две составляющие – нормальную и тангенциальную по отношению к направлению магнитной индукции B, как было показано в вышеуказанной статье. Нормальная составляющая скорости vn обусловливает наводимую ЭДС индукции и равна:
vn = v × sin α ;
Тангенциальная составляющая скорости vt не принимает участия в создании индуктированной ЭДС и равна:
vt = v × cos α ;
при α = 90° нормальная скорость
vn = v × sin α = v × sin 90° = v ,
то есть в этом случае нормальная составляющая скорости имеет максимальное значение. Такое же значение имеет в этот момент величина индуктированной ЭДС в проводнике:
e = B × l × v = Em ,
откуда общее выражение для ЭДС в проводнике будет:
e = Em × sin α или e = sin α .
При движении проводник будет занимать различные положения. На чертеже положения проводника даны через каждые 45° угла поворота. Рассматривая отдельные положения проводника, мы видим, что угол пересечения α меняется и, кроме того, при переходе проводника через нейтральную линию направление индуктированной ЭДС, определяемое по правилу правой руки, также меняется. Для наглядности составим таблицу зависимости величины и направления ЭДС (пропорциональной sin α) от положения проводника и угла между векторами индукции и скорости вращения проводника (таблица 1).
Таблица 1
Зависимость величины и направления ЭДС от положения проводника
| Положение проводника | Угол α между векторами индукции B и скорости v | Sin α | Направление ЭДС в проводнике |
| 1 2 3 4 5 6 7 8 9 или 1 | 0 45 90 135 180 225 270 315 360 | 0 0,707 1 0,707 0 – 0,707 – 1 – 0,707 0 | – К нам К нам К нам – От нас От нас От нас – |
Из таблицы видно, что за один полный оборот проводника ЭДС в нем сначала увеличивается от нуля до максимального значения, затем уменьшается до нуля и, изменив свое направление, вновь увеличивается до максимального значения и вновь уменьшается до нуля. При дальнейшем движении проводника изменения ЭДС будут повторяться.
Для наглядного представления о ходе изменения индуктированной ЭДС в проводнике воспользуемся графическим методом. Проведем две взаимно перпендикулярные оси (рисунок 1, б). На горизонтальной оси в одном масштабе отложим углы поворота проводника, а на вертикальной в другом масштабе – величину ЭДС, индуктированную в проводнике в каждый момент времени. Если ЭДС, индуктированную в проводнике при прохождении его под южным полюсом, считать положительной и откладывать от горизонтальной оси вверх, то ЭДС индуктированную в проводнике при прохождении его под северным полюсом, следует считать отрицательной и откладывать от горизонтальной оси вниз. Проведя затем через концы отрезков, изображающих в масштабе величины ЭДС, непрерывную линию, получим кривую, называемую синусоидой. При помощи кривой мы можем легко определить ЭДС в любой момент времени. Для этого на горизонтальной оси откладываем интересующий нас угол поворота проводника от начального положения. Затем от этой точки восстанавливаем перпендикуляр. Отрезок, заключенный между точками пересечения перпендикуляра с кривой и горизонтальной осью, будет в масштабе выражать величину индуктированной ЭДС в проводнике в этот момент времени.
В нашем примере проводник вращается в однородном магнитном поле. В проводнике индуктировалась ЭДС, изменяющаяся по закону синуса. Такая ЭДС называется синусоидальной.
В дальнейших статьях мы увидим, что электротехника предпочитает пользоваться переменными величинами, изменяющимися по синусоидальному закону.
Рассмотрим принцип получения синусоидальной ЭДС. Устройство, показанное на рисунке 2, позволяет снимать и отводить во внешнюю цепь переменную ЭДС. Согнутый рамкой проводник вращается в магнитном поле под действием посторонней силы. Концы рамки присоединены к двум медным кольцам 3 и 4, на которые наложены две угольные щетки 5 и 6. Во внешней цепи будет протекать изменяющийся по величине и направлению ток. Такой ток называется переменным в отличие от постоянного, который дают гальванические элементы и аккумуляторы. Переменный ток на электрических схемах принято обозначать условным знаком ~ .
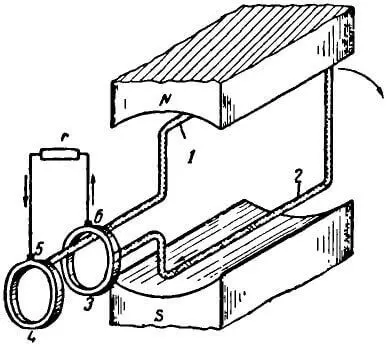
Рисунок 2. Устройство для отвода переменного тока от ротора генератора
В создании индуктированной ЭДС будут участвовать не все стороны рамки, а лишь те, которые пересекают магнитные линии. Эти стороны называются активными сторонами (на рисунке 2 они обозначены цифрами 1 и 2).
Конструкция генератора переменного тока, показанная на рисунке 2, не может быть практически использована. Недостатком ее является трудность создания однородного магнитного поля и большое магнитное сопротивление магнитному потоку, который значительный путь проходит по воздуху.
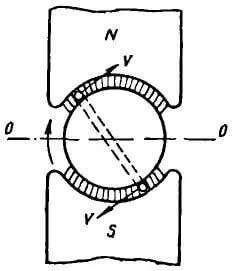
при наличии стального барабана
В конструкциях современных электрических машин между полюсами электромагнита помещают стальной барабан, в пазы которого укладывают проводники обмотки. Такая конструкция машины представлена на рисунке 3. Магнитным линиям в этом случае приходится проходить по воздуху короткий путь между сталью полюсов и барабана. Можно доказать, что магнитные линии, проходя воздушный промежуток, будут входить в барабан в радиальном направлении и в таком же направлении будут выходить из него, чтобы попасть в другой полюс. В этом случае направление окружной скорости в каждый момент перпендикулярно направлению магнитных линий, то есть скорость будет все время нормальной скоростью (v = vn).
Стремление получить синусоидальную ЭДС заставляет конструктора машины придать такую форму полюсным наконечникам, при которой магнитная индукция в воздушном зазоре изменялась бы по закону синуса:
B = Bm × sin α ,
где Bm – максимальная магнитная индукция в воздушном зазоре при α = 90°, то есть
B = Bm × sin α = B = Bm × sin 90° = Bm .
В этот момент ЭДС, индуктированная в проводнике, также имеет максимальное значение:
e = Bm × l × v = Em ,
откуда общее выражение для ЭДС в проводнике будет:
e = Em × sin α
или
e = sin α .
Для получения индуктированной ЭДС в генераторах безразлично, будет ли движущийся проводник пересекать неподвижное магнитное поле или движущееся поле будет пересекать неподвижный проводник. В рассмотренных конструкциях генераторов переменного тока обмотка, где индуктировалась переменная ЭДС, размещалась на вращающейся части машины – роторе, а полюса располагались на неподвижной части машины – статоре. Однако для того чтобы поставить обмотку переменного тока в более благоприятные условия, ее чаще располагают на статоре, а обмотку возбуждения полюсов помещают на роторе. Генератор такой конструкции представлен на рисунке 4.
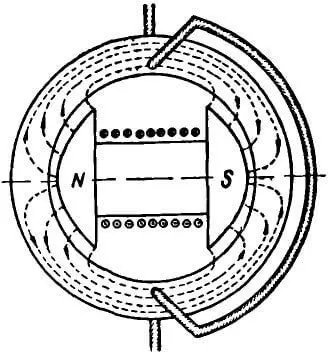
Рисунок 4. Получение синусоидального переменного тока в двухполюсном генераторе
Постоянный ток, необходимый для обмотки возбуждения, подается от специального генератора-возбудителя постоянного тока, сидящего на одном валу с генератором переменного тока, или от выпрямительного устройства.
Источник: Кузнецов М. И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560 с.