Намагничивающая сила поперечной реакции якоря
Рассмотрим вопросы количественного учета влияния реакции якоря на магнитный поток машины. При этом для простоты примем следующие допущения: 1) якорь не имеет пазов, однако влияние пазов на магнитное сопротивление зазора учитывается введением в рассмотрение эквивалентного воздушного зазора δ’ = kδ × δ ; 2) проводники якоря распределены равномерно по окружности якоря. Получаемые при этом результаты достаточно точны для практических целей.
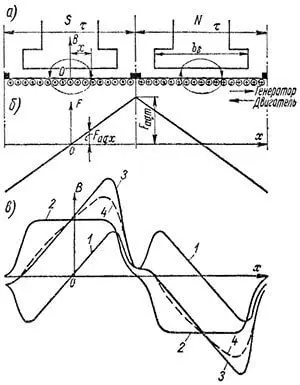
На рисунке 1, а изображена машина в развернутом виде на протяжении двойного полюсного деления, причем щетки установлены на геометрической нейтрали. Характер возникающего поля поперечной реакции якоря также показан на рисунке. Величины, относящиеся к поперечной реакции якоря, будем обозначать индексами aq, а к продольной реакции – индексами ad.
Применим закон полного тока
![]()
к линии магнитной индукции, пересекающей зазор в пределах полюсного наконечника на расстоянии x от центра полюса, и предположим сначала, что в стальных участках магнитной цепи μс = ∞ и поэтому в стали H = 0. Можно принять также, что вдоль магнитной линии в воздушном зазоре Haqx = const. Тогда вместо указанного интегрального соотношения получим
2 × Haqx × δ’ = 2 × Aa × x ,
где Aa – линейная нагрузка якоря.
Таким образом,
![]()
Это соотношение можно представить в виде
| Baqx = λx × Faqx , | (1) |
где
| λx = μ0 /δ’ | (2) |
представляет собой магнитную проводимость зазора на единицу площади, а
| Faqx = Aa × x | (3) |
– намагничивающую силу поперечной реакции якоря в точке с координатой x.
На основании соотношения (3) можно построить зависимость Faqx = f(x), причем надо учесть, что при изменении направления тока в проводниках якоря Aa меняет знак (рисунок 1, б). Максимальное значение Faqx достигается на линии геометрической нейтрали:
| (4) |
а возле края полюсного наконечника
| Faqb = Aa × bδ / 2 . | (5) |
Размагничивающее действие поперечной реакции якоря
При λx = const кривая индукции Baqx повторяла бы кривую Faqx. Однако в междуполюсном пространстве λx уменьшается, и Baqx = f(x) принимает форму кривой 1 на рисунке 1, в. На этом же рисунке кривая 2 представляет собой распределение индукции поля возбуждения в зазоре. Кривая индукции результирующего поля 3 получается при отсутствии насыщения путем сложения ординат кривых 1 и 2. В действительности в следствие насыщения магнитной цепи результирующая индукция на тех участках, где поля складываются, будет меньше арифметической суммы ординат кривых 1 и 2, а на участках где поля вычитаются, – больше арифметической разности ординат кривых 1 и 2. Поэтому с учетом насыщения кривая индукции результирующего поля примет вид штриховой кривой 4.
При отсутствии насыщения поперечная реакция якоря вызывает лишь искажение кривой поля в зазоре, однако поток одного полюса остается неизменным. Но при наличии насыщения уменьшение потока на том краю полюса, где поля вычитаются, будет больше, чем увеличение на том краю полюса, где поля складываются. Это объясняется тем, что насыщение сильнее там, где сильнее результирующее поле.
Вследствие этого под влиянием насыщения поперечная реакция якоря всегда вызывает некоторое уменьшение потока полюсов, и в этом смысле говорят, что поперечная реакция якоря действует размагничивающим образом.
Следует отметить, что в некоторых случаях в машинах мощностью 30 – 40 кВт при номинальной нагрузке, а также в других машинах в таких режимах работы, когда поток возбуждения ослаблен, под воздействием реакции якоря возможно изменение направления ("опрокидывание") поля под одним краем полюса. При Pн > 50 кВт значение δ обычно выбирают таким, чтобы при номинальной нагрузке не происходило "опрокидывания" поля. С этой же целью в мощных машинах зазор под краями полюсных наконечников делают больше, чем под центром полюса. Это приводит также к улучшению условий коммутации сложных обмоток, так как распределение индукции поля возбуждения приближается к синусоидальному и электродвижущая сила от высших гармоник поля, которые могут вызвать большие разности напряжений между соседними коллекторными пластинами многоходовых петлевых обмоток, уменьшается.
Количественный учет влияния поперечной реакции якоря
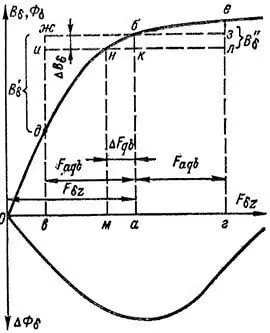
Насыщение полюсных наконечников и тела якоря невелико, и поэтому при количественном учете влияния поперечной реакции якоря достаточно учесть лишь насыщение зубцов. Для такого учета по данным расчета магнитной цепи при холостом ходе строят так называемую переходную магнитную характеристику машины (рисунок 2), представляющую собой зависимость индукции в воздушном зазоре Bδ при холостом ходе от суммы намагничивающих сил зазора и зубцов: Fδz = Fδ + Fz.
Пусть при холостом ходе Bδ определяется ординатой аб на рисунке 2. Тогда намагничивающая сила воздушного зазора и зубцового слоя Fδz, создаваемая обмоткой возбуждения, будет равна абсциссе 0а. Согласно изложенному выше (смотрите рисунок 1), при нагрузке по центральной осевой линии полюсного наконечника (координата x = 0 на рисунке 1) действует такая же намагничивающая сила, однако в других точках воздушного зазора будет действовать намагничивающая сила
| Fвa = Fδz + Faqx = Fδz + Aa × x . | (6) |
Если отложить на рисунке 2 от точки а вправо и влево намагничивающую силу Faqb, вычисленную по формуле (5), то действующая в разных точках на протяжении полюсного наконечника намагничивающая сила Fвa будет равна абсциссам точек отрезка ваг, а индукция результирующего поля в зазоре в этих точках на протяжении полюсного наконечника определится ординатами участка кривой дбе.
Отрезок вг на рисунке 2 пропорционален ширине полюсного наконечника, и поэтому площадь фигуры вдбегав пропорциональна потоку полюса при нагрузке. В то же время площадь прямоугольника вжзг пропорциональна потоку полюса при холостом ходе. Поэтому площадь криволинейного треугольника без характеризует увеличение потока под одной половиной полюса, а площадь треугольника джб – его уменьшение под другой половиной полюса. Таким образом, разность площадей этих треугольников определяет уменьшение потока полюса под влиянием поперечной реакции якоря.
Заменим на рисунке 2 фигуру вдбегав равновеликим ей по площади прямоугольником вилг. Тогда ордината ак представляет собой среднюю индукцию Bδн в воздушном зазоре при нагрузке, а отрезок бк = ΔBδ – уменьшение средней индукции при нагрузке. По данным расчета магнитной цепи при холостом ходе можно отложить по оси ординат вместо Bδ пропорциональное ей значение потока Фδ в воздушном зазоре. Тогда отрезок бк = ΔФδ непосредственно определяет уменьшение потока полюса под воздействием поперечной реакции якоря.
Отрезок ма = ΔFqb на рисунке 2 представляет собой значение намагничивающей силы возбуждения, эквивалентное размагничивающему действию поперечной реакции якоря. Соответствующим увеличением намагничивающей силы возбуждения размагничивающее действие реакции якоря может быть скомпенсировано.
Если перемещать точку а на рисунке 2 при Faqb = const вдоль оси абсцисс, то есть рассматривать влияние поперечной реакции при разных условиях насыщения, то ΔФδ будет изменяться так, как показано в нижней части рисунка 2. Значение ΔФδ максимально для точки, соответствующей колену переходной характеристики, и уменьшается от этой точки в обе стороны. Таким образом, влияние поперечной реакции якоря при Ia = const зависит от положения рабочей точки на магнитной характеристике машины.
При неизменной намагничивающей силе возбуждения зависимость ΔFqb и ΔФδ от Ia является сложной функцией. Однако при изменении Ia в небольших пределах в области номинальной нагрузки можно без особой погрешности принять, что ΔFqb ~ Ia.
Подсчет площадей криволинейных треугольников вида джб и без на рисунке 2 трудоемок. Поэтому различными авторами предложены более удобные методы определения ΔФδ и ΔFqb.
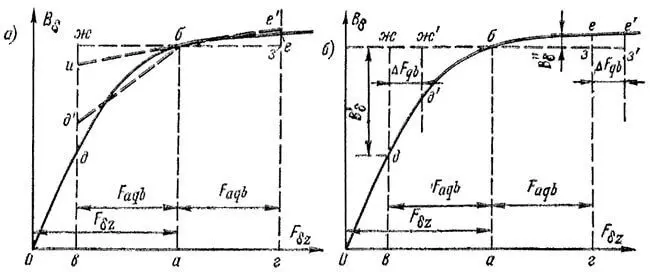
Метод В. Т. Касьянова предусматривает проведение (рисунок 3, а) прямых д’б и бе’ таким образом, чтобы были соответственно равны площади треугольников джб и д’жб и площади треугольников без и бе’з. Достаточно точное проведение таких прямых возможно по глазомерной оценке. Затем прямая бе’ продолжается до пересечения с линией вж в точке и. Тогда ΔФδ определяется площадью треугольника д’иб и
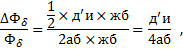
откуда нетрудно найти ΔФδ и затем соответствующее значение ΔFqb.
Рисунок 3. Определение размагничивающего действия поперечной реакции якоря:
а – по методу В. Т. Касьянова; б – по методу Г. Н. Петрова
Метод Г. Н. Петрова исходит из определения площади фигур, ограниченных кривыми параболического характера, по формуле Симпсона. При этом поток при нагрузке (рисунок 3, б)
![]()
и уменьшение потока
![]()
С другой стороны, если увеличить намагничивающую силу возбуждения на ΔFqb (рисунок 3, б), чтобы скомпенсировать таким образом влияние реакции якоря, это будет соответствовать увеличению потока на сумму площадей криволинейных прямоугольников джж’д’ и зее’з’, которая приближенно равна
ΔФδ = жд × ΔFqb + ез × ΔFqb = (B’δ + B’’δ) × ΔFqb .
Приравнивая два выражения для ΔФδ, имеем
| (7) |
Более точные результаты можно получить, если вычислить сначала ΔFqb по формуле (7), отложить это значение ΔFqb на рисунок 3, б от точек в и г вправо и вычислить затем ΔFqb снова, подставив в выражение (7) вместо B’δ и B’’δ полусуммы (дж + д’ж’) / 2 и (зе + з’е’) / 2.
Учет реакции якоря при сдвиге щеток
Сдвиг щеток с геометрической нейтрали, измеряемый длиной дуги
c = α × Da / 2
по окружности якоря (смотрите рисунок 4, в статье "Реакция якоря и ее виды"), обычно невелик, так что τ – 2c > bδ. При этом намагничивающая сила продольной реакции якоря на один полюс
| Fad = c × Aa | (8) |
в зависимости от ее направления непосредственно складывается с намагничивающей силой возбуждения или вычитается из нее. В результате получается намагничивающая сила по продольной оси
| Fd = Fв ± Fad . | (9) |
Для компенсации продольной оси реакции якоря в этом случае достаточно увеличить или уменьшить Fв на величину Fad в зависимости от того, является ли действие Fad размагничивающим или намагничивающим. При таком методе не учитывается погрешность, связанная с тем, что поток рассеяния полюсов создается не намагничивающей силой Fd, а намагничивающей силой Fв. Однако эта погрешность невелика.
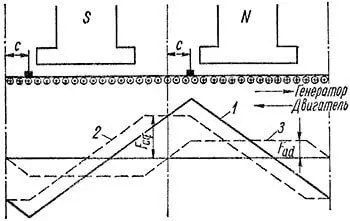
Учет размагничивающего действия поперечной реакции якоря в рассматриваемом случае производится так же, как и при c = 0. Диаграмма намагничивающей силы якоря для этого случая показана на рисунке 4, где кривые 1, 2 и 3 представляют собой соответственно полную, поперечную и продольную намагничивающие силы реакции якоря.
Если τ – 2c < bδ, то учет влияния реакции якоря несколько усложняется. Этот случай в нормальных машинах на практике не встречается и поэтому здесь подробнее не рассматривается.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.