Решение вопросов, связанных с параллельным соединением цепей переменного тока, так же как и при постоянном токе, производится при помощи проводимостей.
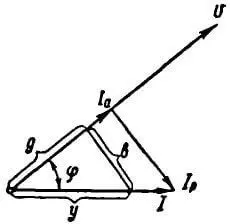
Рисунок 1. Разложение тока на активную и реактивную составляющую
Пусть мы имеем векторную диаграмму, изображенную на рисунке 1. Проектируя вектор тока I на направление вектора напряжения U, разложим вектор тока на две составляющие.
Одна из составляющих совпадает по направлению с вектором напряжения и называется активной составляющей тока. Она обозначается буквой Iа и равна:
Iа = I × cos φ .
Другая составляющая, перпендикулярная вектору напряжения, называется реактивной составляющей тока, обозначается Iр и равна:
Iр = I × sin φ .
Итак, активная и реактивная составляющие тока представляют собой компоненты полного тока.
По закону Ома для цепей переменного тока имеем:
![]()
Из прямоугольника сопротивлений легко получить:
![]()
Используя эти три выражения, получим:
![]()
По аналогии с формулой постоянного тока (I = U × g) заменим в ней ![]() на g. Полученная формула будет иметь следующий вид:
на g. Полученная формула будет иметь следующий вид:
Iа = U × g .
Величина g называется активной проводимостью.
Соответственно изложенному, получим:
![]()
Обозначив ![]() через b, получим:
через b, получим:
Iр = U × b .
Величина b называется реактивной проводимостью.
Наконец,
![]()
Обозначив ![]() через y, получим:
через y, получим:
I = U × y .
Величина y называется полной проводимостью.
Активная проводимость, реактивная проводимость и полная проводимость измеряются в ![]() .
.
На рисунке 1 изображен треугольник токов со сторонами I, Iа, Iр.
По теореме Пифагора имеем:
![]()
Разделив все стороны треугольника токов на U:
![]()
Получим треугольник проводимостей со сторонами g, b и y .
Из треугольника проводимостей имеем:
![]()
Источник: Кузнецов М. И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560 с.