Комбинированная, или лягушечья, обмотка впервые была предложена Латуром в 1910 году и представляет собой сочетание петлевой и волновой обмоток, которые расположены в общих пазах, присоединяются к общему коллектору и работают параллельно.
Так как каждая из обмоток двухслойная, то в пазу располагаются четыре слоя обмотки. Каждая из обмоток рассчитывается на половину общего тока, а их электродвижущие силы должны быть равны. Таким образом, каждая обмотка рассчитывается на половину мощности машины.
Рассмотрим условия выполнения симметричной комбинированной обмотки при минимально возможном числе ветвей. Величины, относящиеся к петлевой и волновой обмоткам, будем при этом писать соответственно с индексом "п" и "в".
Петлевая обмотка имеет минимальное число ветвей в случае, если она простая. Тогда mп = 1, aп = p и, согласно соотношению (5), представленному в статье "Общие сведения о якорных обмотках машин постоянного тока",
 |
| Рисунок 1. Два варианта выполнения комбинированной обмотки |
K / p = целое число
При этом на основании формулы (3), представленной в статье "Сложная волновая обмотка", должны быть
aв / p = mв / p = целое число
Следовательно, минимальное число ветвей волновой обмотки aв = mв = p = aп.
Таким образом, петлевая и волновая обмотки должны иметь равные числа параллельных ветвей. Чтобы электродвижущие силы ветвей были равны, должны быть равны также числа витков ветвей обеих обмоток, а следовательно, и общее число проводников в каждой обмотке. Из условия равенства токов следует, что сечения проводников обеих обмоток также должны быть одинаковы.
Поскольку при mп > 2 петлевая обмотка уже не является симметричной, то возможны только два варианта симметричной комбинированной обмотки: 1) mп = 1, mв = p; 2) mп = 2, mв = 2×p.
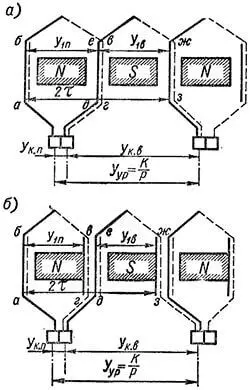
Так как петлевая и волновая обмотки присоединяются к общим коллекторным пластинам, то необходимо иметь определенные соотношения между шагами обмоток, чтобы не возникали уравнительные токи. Существуют два варианта этих соотношений (рисунок 1).
В схеме Латура, изображенной на рисунке 1, а,
| y1п + y1в = K / p ; yк.п + yк.в = K / p . | (1) |
Для предотвращения возникновения уравнительных токов в схеме рисунка 1, а электродвижущая сила в контуре абвгдежз, замкнутом через щетки и соединительную шину между ними, должна равняться нулю. Это условие соблюдается, так как проводники де и гв лежат в одном пазу и имеют равные по значению и направлению электродвижущие силы, а проводники аб и жз также имеют равные по значению и направлению электродвижущие силы, поскольку они сдвинуты в магнитном поле на два полюсных деления.
Схему Латура-Перре (рисунок 1, б) можно получить из схемы Латура (рисунок 1, а), если в последней шаги y1п и y1в являются полными:
и если проводники гв и жз перенести влево на одно зубцовое деление, то есть укоротить шаги y1п и y1в на одно зубцовое деление. Очевидно, что при этом сумма электродвижущих сил в контуре абвгдежз также будет равна нулю.
Для схемы рисунка 1, б существуют следующие соотношения между шагами:
| y1в = y1п ; yк.п + yк.в = K / p . | (2) |
Потенциальный шаг по коллектору
yп = K / p .
Если выполнить на коллекторе уравнительные соединения с таким шагом, то они будут служить в качестве уравнителей первого рода для петлевой обмотки и одновременно уравнителями второго рода для петлевой (если она сложная) и волновой обмоток. Однако, как следует из рисунка 1, а и б, коллекторные пластины, расположенные на расстоянии шага yп, соединяются контуром абвгдежз секций петлевой и волновой обмоток, причем сумма электродвижущих сил этого контура при равенстве потоков полюсов равна нулю. Следовательно, сам этот контур играет роль уравнителя, и поэтому надобности в специальном уравнительном соединении нет.
 |
| Рисунок 2. Форма катушки комбинированной обмотки |
Таким образом, комбинированная обмотка не нуждается в особых уравнителях, так как их роль выполняют элементы самой обмотки. Это является преимуществом обмоток такого типа в случаях, когда требуется наличие полного или большого числа уравнителей. Вместе с тем комбинированные обмотки сложны по конструктивному исполнению, охлаждение их лобовых частей хуже, а их естественные контуры для уравнительных токов имеют повышенную индуктивность, что ухудшает коммутацию. Поэтому применение этих обмоток ограничено.
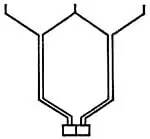
Секции комбинированной обмотки часто объединяют в катушки, форма которых показана на рисунке 2. Вследствие такой формы катушек комбинированную обмотку часто называют лягушечьей.
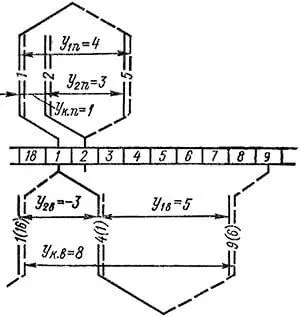
Рассмотрим пример комбинированной обмотки с данными: 2×p = 4, aп = aв = 2, Z = Zэ = S = K =18. Петлевая обмотка является простой, а волновая обмотка – двухходовой двукратнозамкнутой.
 |
| Рисунок 3. Элементы схемы комбинированной обмотки с 2×p = 4, aп = aв = 2, Z = Zэ = S = K = 18 |
Шаги петлевой обмотки:
yк.п = +1 ;
y2п = yк.п – y1п = 1 – 4 = – 3 .
Шаги волновой обмотки:
y2в = yк.в – y1в = 8 – 5 = 3 .
Условия (1) выполняются.
Элементы схемы обмотки изображены на рисунке 3, причем петлевая и волновая обмотки показаны по разным сторонам от коллектора.
Входящие в рассматриваемую комбинированную обмотку простая петлевая и сложная волновая обмотки имеют те же данные, что и обмотки, рассмотренные в статьях "Простая петлевая обмотка" (смотрите рисунки 2, 3 и 5) и "Сложная волновая обмотка" (смотрите рисунки 1, 2 и 3), и поэтому полная схема ее представляет собой сочетание схем 3, статьи "Простая петлевая обмотка", и 2, статьи "Сложная волновая обмотка". Векторные диаграммы на рисунке 5, в статье "Простая петлевая обмотка", и рисунке 3, в статье "Сложная волновая обмотка", одинаковы, что свидетельствует о правильном выборе данных комбинированной обмотки и о ее хороших рабочих свойствах.
При сравнении схем рисунка 2, в статье "Сложная волновая обмотка", и рисунка 3, данной статьи, следует иметь в виду, что на рисунке 2, в статье "Сложная волновая обмотка", нумерация пазов выполнена так, как показано в нижней части рисунка 3 в скобках.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.