Двигатели постоянного тока находят широкое применение в промышленных, транспортных и других установках, где требуется широкое и плавное регулирование скорости вращения (прокатные станы, мощные металлорежущие станки, электрическая тяга на транспорте и так далее).
По способу возбуждения двигатели постоянного тока подразделяются аналогично генераторам на двигатели независимого, параллельного, последовательного и смешанного возбуждения.
Схемы двигателей и генераторов с данным видом возбуждения одинаковы (рисунок 1 в статье "Общие сведения о генераторах постоянного тока") . В двигателях независимого возбуждения токи якоря Iа и нагрузки I равны: I = Iа, в двигателях параллельного и смешанного возбуждения I = Iа + iв и в двигателях последовательного возбуждения I = Iа = Iв.
С независимым возбуждением от отдельного источника тока обычно выполняются мощные двигатели с целью более удобного и экономичного регулирования тока возбуждения. По своим свойствам двигатели независимого и параллельного возбуждения почти одинаковы, и поэтому первые ниже отдельно не рассматриваются.
Энергетическая диаграмма
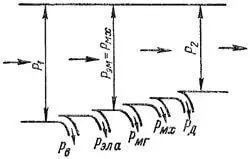
Энергетическая диаграмма двигателя параллельного возбуждения изображена на рисунке 1. Первичная мощность P1 является электрической и потребляется из питающей сети. За счет этой мощности покрываются потери на возбуждения pв и электрические потери pэла = Iа² × Rа в цепи якоря, а оставшаяся часть составляет электромагнитную мощность якоря Pэм = Eа × Iа, которая превращается в механическую мощность Pмх. Потери магнитные pмг, добавочные pд, и механические pмх покрываются за счет механической мощности, а остальная часть этой мощности представляет собой полезную механическую мощность P2 на валу.
Аналогичные энергетические диаграммы, иллюстрирующие преобразование энергии в двигателе, можно построить и для других типов двигателей.
Уравнение вращающих моментов
Электромагнитный момент двигателя
Mэм = Pэм / Ω,
который является движущим и действует в сторону вращения, расходуется на уравновешивание тормозящих моментов: 1) момента M0, соответствующего потерям pмг, pд и pмх, покрываемым за счет механической мощности [смотрите равенство (6) в статье "Общие сведения о генераторах постоянного тока"]; 2) Mв – момента нагрузки на валу, создаваемого рабочей машиной или механизмом; 3) Mдин – динамического момента [смотрите равенство (7) в статье "Общие сведения о генераторах постоянного тока"]. При этом
Mв = P2 /Ω
Таким образом,
| Mэм = M0 + Mв + Mдин | (1) |
или
| Mэм = Mст + Mдин | (2) |
где
Mст = M0 + Mв
является статическим моментом сопротивления.
При установившемся режиме работы, когда n = const и поэтому Mдин = 0,
| Mэм = Mст. | (3) |
В дальнейшем индекс "эм" у Mэм будем опускать. Обычно M0 мал по сравнению с Mв, и поэтому приблизительно можно считать, что при установившемся режиме работы Mэм = M является полезным моментом на валу и уравновешивается моментом Mв. Можно также значение M0 включить в значение Mв.
Укажем, что если выразить P в киловаттах, а Ω - через число оборотов в минуту nм, то между P, nм и M в кгс × м будет существовать зависимость
![]()
Уравнение напряжения и тока
В двигателях направление действия э. д. с. якоря Eа противоположно направлению тока якоря Iа (смотрите статью "Принцип действия машины постоянного тока"), и поэтому Eа называется также противоэлектродвижущей силой якоря. Уравнение напряжения для цепи якоря двигателя можно записать следующим образом:
| U = Eа + Rа × Iа. | (4) |
Здесь Rа – полное сопротивление цепи якоря [смотрите равенство (15) в статье "Общие сведения о генераторах постоянного тока"]. В режиме двигателя всегда U > Eа.
Из равенства (4) следует, что
| (5) |
где, согласно выражению (3), в статье "Основные электромагнитные соотношения. Электродвижущая сила якоря и электромагнитный момент",
| Eа = cе × Фδ × n. | (6) |
Скорость вращения и механические характеристики
Решая уравнение (4) совместно с (6) относительно n, находим уравнение скоростной характеристики n = f(Iа) двигателя:
| (7) |
Согласно выражению (8), в статье "Основные электромагнитные соотношения. Электродвижущая сила якоря и электромагнитный момент",
| M = см × Фδ × Iа. | (8) |
Определив отсюда значение Iа и подставив его в (7), получим уравнение механической характеристики n = f(M) двигателя:
| (9) |
которое определяет зависимость скорости вращения двигателя от развиваемого момента вращения.
Вид механической характеристики n = f(M) или M = f(n) при U = const зависит от того, как с изменением момента M изменяется поток машины Фδ, и различен для двигателей с различными способами возбуждения. Это же справедливо для скоростных характеристик (смотрите статьи "Двигатели параллельного возбуждения", "Двигатели последовательного возбуждения", "Двигатели смешанного возбуждения").
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.