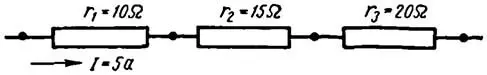Первый закон Кирхгофа

Информация о материале: Категория: Статьи; Опубликовано: 14 августа 2013; Просмотров: 314

Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно. При этом последовательное и параллельное соединение проводников являются основными видами соединений, а смешанное соединение это их совокупность.

Последовательное соединение проводников

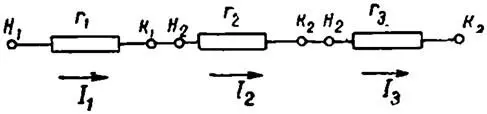
Последовательным соединением проводников называется такое соединение, когда конец первого проводника соединен с началом второго, конец второго проводника соединен с началом третьего и так далее (рисунок 1).

Рисунок 1. Схема последовательного соединения проводников

Общее сопротивление цепи, состоящее из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:

r = r₁ + r₂ + r₃ + … + r_n.

Ток на отдельных участках последовательной цепи везде одинаков:

I₁ = I₂ = I₃ = I.

Видео 1. Последовательное соединение проводников

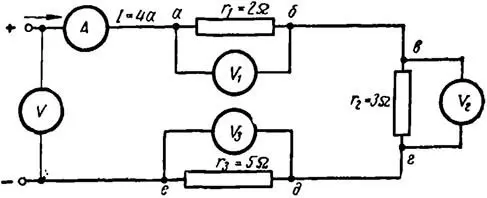
Пример 1. На рисунке 2 представлена электрическая цепь, состоящая из трех последовательно включенных сопротивлений r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 5 Ом. Требуется определить показания вольтметров V₁, V₂, V₃ и V₄, если ток в цепи равен 4 А.

Сопротивление всей цепи

r = r₁ + r₂ + r₃ = 2 + 3 + 5 =10 Ом.

По закону Ома напряжение на зажимах цепи равно току цепи, умноженному на ее сопротивление:

U = I × r = 4 × 10 = 40 В.

Следовательно, вольтметр V, присоединенный к зажимам источника напряжения, покажет напряжение 40 В.

Рисунок 2. Схема измерения напряжений на отдельных участках электрической цепи

В сопротивлении r₁ при протекании тока будет падение напряжения:

U₁ = I × r₁ = 4 × 2 = 8 В.

Вольтметр V₁, включенный между точками а и б, покажет 8 В.

В сопротивлении r₂ также происходит падение напряжения:

U₂ = I × r₂ = 4 × 3 = 12 В.

Вольтметр V₂, включенный между точками в и г, покажет 12 В.

Падение напряжения в сопротивлении r₃:

U₃ = I × r₃ = 4 × 5 = 20 В.

Вольтметр V₃, включенный между точками д и е, покажет 20 В.

Если вольтметр присоединить одним концом к точке а, другим концом к точке г, то он покажет разность потенциалов между этими точками, равную сумме падений напряжения в сопротивлениях r₁ и r₂ (8 + 12 = 20 В).

Таким образом, вольтметр V, измеряющий напряжение на зажимах цепи и включенный между точками а и е, покажет разность потенциалов между этими точками или сумму падений напряжения в сопротивлениях r₁, r₂ и r₃.

Отсюда видно, что сумма падений напряжения на отдельных участках электрической цепи равна напряжению на зажимах цепи.

Так как при последовательном соединении ток цепи на всех участках одинаков, то падение напряжения пропорционально сопротивлению данного участка.

Пример 2. Три сопротивления 10, 15 и 20 Ом соединены последовательно, как показано на рисунке 3. Ток в цепи 5 А. Определить падение напряжения на каждом сопротивлении.

U₁ = I × r₁ = 5 ×10 = 50 В,
U₂ = I × r₂ = 5 ×15 = 75 В,
U₃ = I × r₃ = 5 ×20 = 100 В.

Рисунок 3. К примеру 2

Общее напряжение цепи равно сумме падений напряжений на отдельных участках цепи:

U = U₁ + U₂ + U₃ = 50 + 75 + 100 = 225 В.

Параллельное соединение проводников

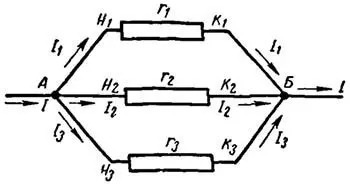
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.

Рисунок 4. Схема параллельного соединения проводников

Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:

I = I₁ + I₂ + I₃.

Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:

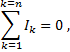
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.

Видео 2. Первый закон Кирхгофа

Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.

Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.

Общий ток, приходящий к точке А, равен:

Токи в каждой из ветвей имеют значения:

По формуле первого закона Кирхгофа

I = I₁ + I₂ + I₃

или

Вынося U в правой части равенства за скобки, получим:

Сокращая обе части равенства на U, получим формулу подсчета общей проводимости:

или

g = g₁ + g₂ + g₃.

Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.

Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 4 Ом.

откуда

Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:

откуда

Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.

Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r₁, деленному на число ветвей n:

Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:

Для проверки попробуем найти сопротивление разветвления по формуле:

откуда

Как видим, ответ получается тот же.

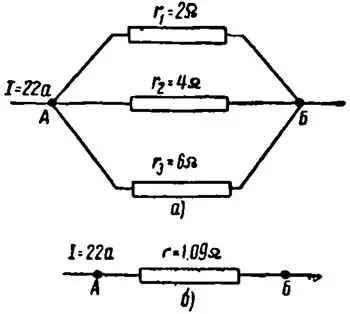
Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а.

Сопротивление проводника при параллельном соединении

Рисунок 5. К примеру 6

Найдем общее сопротивление цепи:

откуда

Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б).

Падение напряжения на участке между точками А и Б будет:

U = I × r = 22 × 1,09 = 24 В.

Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б.

Рассматривая первую ветвь разветвления с сопротивлением r₁, мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:

Ток второй ветви

Ток третьей ветви

Проверим по первому закону Кирхгофа

I = I₁ + I₂ + I₃ = 12 + 6 + 4 = 22 А.

Следовательно, задача решена верно.

Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения.

Первая ветвь: r₁ = 2 Ом, I₁ = 12 А.
Вторая ветвь: r₂ = 4 Ом, I₂ = 6 А.
Третья ветвь: r₃ = 6 Ом, I₃ = 4 А.

Как видим, сопротивление первой ветви в два раза меньше сопротивление второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.

Для двух параллельных ветвей можно также, конечно, пользоваться данной выше формулой.

Однако общее сопротивление проводника при параллельном соединении в этом случае легче подсчитать по формуле:

или окончательно:

Смешанное соединение проводников

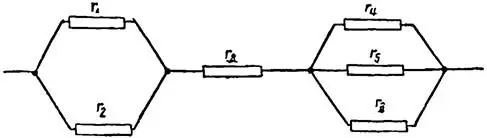
Смешанным соединением проводников называется такое соединение, где имеются и последовательное и параллельное соединения отдельных проводников. Примером может служить соединение, изображенное на рисунке 6.