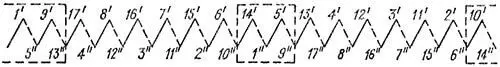Общие положения
 |
| Рисунок 1. Секции неперекрещенной (а) и перекрещенной (б) простой волновой обмотки |
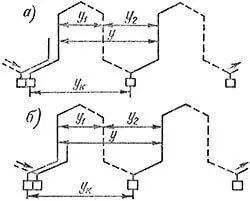
Мысленно обходя последовательно соединенные секции простой волновой обмотки, мы совершаем волнообразный обход якоря, причем каждый обход включает p секций и заканчивается на коллекторной пластине, которая находится слева или справа рядом с исходной (рисунок 1). В первом случае (рисунок 1, а), получается неперекрещенная обмотка, а во втором (рисунок 1, б) – перекрещенная. Во втором случае расход меди будет несколько больше. Рассматриваемую обмотку называют также простой последовательной обмоткой.
В соответствии со сказанным между шагом по коллектору yк (рисунок 1) и числом коллекторных пластин K простой волновой обмотки существует зависимость
p × yк ± 1 = K ,
откуда
 | (1) |
Знак минус относится к неперекрещенной обмотке, а знак плюс – к перекрещенной. Поскольку шаг yк = y должен быть целым числом, то K не может принимать произвольных значений.
Шаг y1 определяется по формуле (1), представленной в статье "Электродвижущая сила секций", и выражению
| (2) |
Шаги y1 и y2 близки к τ, а y = yк — к 2×τ.
Симметричная волновая обмотка
Ознакомимся со свойствами простой волновой обмотки на примере обмотки с 2×p = 4 и Z = Zэ = S = K = 17. Возьмем при этом
и
y2 = y – y1 = 8 – 4 = 4 .
Порядок соединений секционных сторон обмотки определяется таблицей на рисунке 2, а схема обмотки имеет вид, показанный на рисунке 3. Ряд секций, выделенных на рисунке 3 жирными линиями, в отличие от секций петлевых обмоток замыкается накоротко через две щетки одной полярности и соединительные провода между ними. Короткозамкнутые секции обведены рамкой также и на рисунке 2
Рисунок 2. Таблица соединений секционных сторон простой волновой обмотки, показанной на рисунке 3
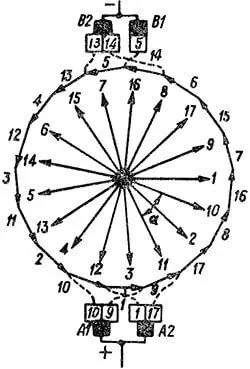
На рисунке 4 построены звезда электродвижущих сил секций и векторная диаграмма электродвижущих сил обмотки, представленной на рисунке 3. Масштаб звезды электродвижущих сил в два раза больше масштаба многоугольника электродвижущих сил.
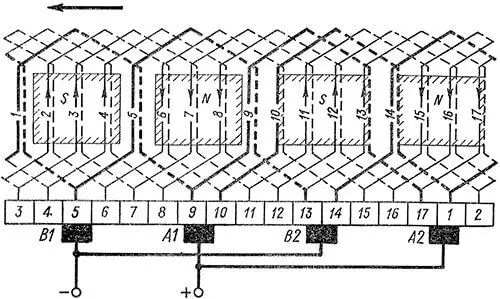
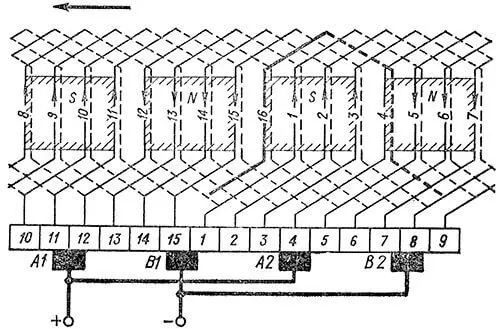
Рисунок 3. Схема простой волновой обмотки с 2×p = 4, Z = Zэ = S = K = 17, y1 = 4, y2 = 4, yк = 8
Как следует из рисунка 2, 3 и 4, обмотка имеет две параллельные ветви. Одна из них содержит секции 17, 8, 16, 7, 15, 6, присоединена своими концами к коллекторным пластинам 17, 14 и расположена, таким образом, между щетками А2, В2. Другая ветвь содержит секции 13, 4, 12, 3, 11, 2, присоединена концами к пластинам 13, 10 и расположена между щетками В2, А1.
Полученный вывод носит общий характер: всякая простая волновая обмотка имеет число параллельных ветвей
| (3) |
и векторная диаграмма электродвижущих сил такой обмотки всегда состоит из одного многоугольника.
Поскольку каждая из ветвей простой волновой обмотки проходит под всеми полюсами, то неравенство потоков полюсов не вызывает неравенства электродвижущих сил и токов параллельных ветвей. Поэтому такая обмотка не нуждается в уравнительных соединениях.
 |
| Рисунок 4. Векторная диаграмма электродвижущих сил обмотки, изображенной на рисунке 3 |
Более того, согласно выражению (5), представленному в статье "Простая петлевая обмотка", и выражению (1), данной статьи, шаг yп в простой волновой обмотке является нецелым числом, и поэтому равнопотенциальных точек не имеется, что видно также из рисунка 4.
При волновой обмотке на коллекторе можно установить только два щеточных пальца, например А1 и В2 на рисунке 3, так как все щетки данной полярности соединены короткозамкнутыми секциями, через которые ток нагрузки распределяется по параллельно работающим щеткам каждой полярности. Два щеточных пальца примут на себя весь ток нагрузки. Эта возможность иногда используется в машинах мощностью до 0,5 кВт, если доступ для ухода за щетками по всей окружности коллектора затруднен. Однако условия коммутации при этом ухудшаются. Кроме того, в более мощных машинах возникает необходимость удлинять коллектор. Поэтому обычно ставится полный комплект (2×p) щеточных пальцев.
При а = 1 условия симметрии, описанные выражениями (5), (6) и (7) в статье "Общие сведения о якорных обмотках машин постоянного тока", удовлетворяются при любых p, Z, uп и K. Однако возможности выбора этих величин ограничиваются соотношением (1), настоящей статьи, которое при подстановке K = uп × Z принимает вид
 | (4) |
Поскольку шаг yк должен быть целым числом, то отсюда видно, что, например, при четных p как Z, так и uп должны быть нечетными (uп = 1, 3, 5…).
Простая волновая обмотка с мертвой секцией
Трудности в соблюдении равенства (1) или (4) в ряде случаев обходят, используя несимметричные обмотки. Например, при четных p и Zэ = uп × Z можно применить обмотку с K = Zэ – 1 и оставить одну секцию неиспользованной, или "мертвой". У этой секции обрезаются концы, и она не присоединяется к коллектору (секция оставляется на якоре, чтобы не нарушать балансировки).
Схема такой обмотки для 2×p = 4, Zэ = 16 и K = 15 показана на рисунке 5, причем принято, что
При обходе обмотки и счете шагов стороны мертвой секции исключаются.
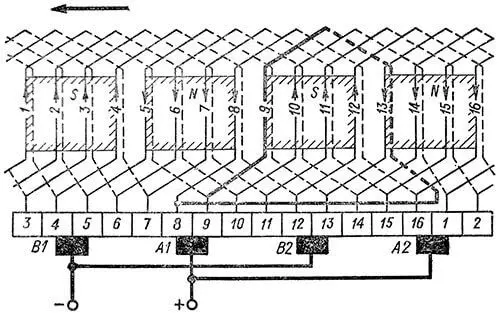
Рисунок 5. Схема простой волновой обмотки с мертвой секцией с 2×p = 4, Z = Zэ = 16, K = 15, y1 = 4, y2 = 4, yк = 8
Искусственно замкнутая простая волновая обмотка
Предположим, что Zэ = S = K = 16 и 2×p = 4. Шаги обмотки выберем из предположения, что Zэ, S и K на единицу больше, то есть Zэ = S = K = 17. При этом, согласно выражению (1), можно взять
Исходя из таких значений шагов, составляем схему обмотки (рисунок 6), начиная, например, с пластины 1. При первом обходе вокруг якоря проходим секции 1 и 1 + 8 = 9 и должны были бы прийти к пластине 9 + 8 = 17. Второй обход должен был бы включать в себя секции 17 и 8. Однако, поскольку секции 17 и пластины 17 нет, то после завершения первого обхода конец секции 9 с помощью обходной перемычки непосредственно соединяем с пластиной 8 и началом секции 8. После этого ход обмотки следует по обычным правилам с тем лишь отличием, что каждый второй результирующий шаг сокращается на единицу.
Рисунок 6. Схема искусственно замкнутой простой волновой обмотки с 2×p = 4, Z = Zэ = S = K = 16, y1 = 4, y2 = 4, yк = 8
Рассмотренные несимметричные волновые обмотки находят применение в машинах мощностью до нескольких десятков киловатт и работают вполне удовлетворительно.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.