Уравнение нагревания
Хотя электрическая машина имеет сложное устройство, в основу анализа процесса ее нагревания может быть положена теория нагревания идеального однородного твердого тела, под которым здесь понимается тело, обладающее равномерным рассеянием тепла со всей поверхности и бесконечно большой теплопроводностью, вследствие чего все точки тела имеют одинаковую температуру. Составим дифференциальное уравнение нагревания такого тела, для чего рассмотрим его тепловой баланс.
Пусть в единицу времени в теле выделяется количество теплоты Q. Тогда за бесконечно малый промежуток времени выделяемое количество теплоты будет равно Q × dt. Эта теплота частично аккумулируется в теле при повышении температуры и частично отдается во внешнюю среду.
Если за время dt температура тела повысилась на dΘ, то количество аккумулируемой за это время теплоты равно G × c × dΘ, где G – масса тела и c – его удельная теплоемкость.
Пусть в рассматриваемом бесконечно малом интервале времени превышение температуры тела над температурой окружающей среды равно Θ. Тогда количество теплоты, отдаваемое в окружающее пространство за время dt вследствие лучеиспускания, конвекции и теплопроводности, будет равно S × λ × Θ × dt, где S – площадь тела и λ – коэффициент теплоотдачи с поверхности.
На основе закона сохранения энергии
| Q × dt = G × c × dΘ + S × λ × Θ × dt . | (1) |
Прежде чем приступить к решению уравнения нагревания (1), несколько преобразуем его.
Установившееся превышение температуры и постоянная времени нагревания
После истечения достаточно длительного времени (теоретически при t = ∞) температура тела достигает установившегося значения. Тогда dΘ = 0 и Θ = Θ∞. Подставив эти значения в выражение (1), получим
Q ×dt = S × λ × Θ∞ × dt ,
откуда
| (2) |
Установившееся превышение температуры Θ∞ тем больше, чем больше выделяется тепла и чем хуже условия ее отдачи, то есть чем меньше S × λ.
Разделим обе части выражения (1) на S × λ, используем равенство (2) и обозначим
| (3) |
Тогда вместо (1) получим
| Θ∞ × dt = T × dΘ + Θ × dt. | (4) |
Размерность всех членов (4) должна быть одинакова – температура, умноженная на время. Поэтому T имеет разность времени, что можно установить также по формуле (3). Величина T называется постоянной времени нагревания тела; согласно формуле (3), она тем больше, чем больше теплоемкость тела G × c и чем меньше интенсивность отдачи тепла, то есть меньше S × λ.
Если определить из равенства (2) S × λ и подставить в (3), то получим еще одно выражение для T:
| (5) |
Числитель этого выражения равен количеству теплоты, накопленной в теле при достижении Θ = Θ∞.
Следовательно, в соответствии с выражением (5) постоянная времени нагревания T равна времени, в течение которого температура достигла бы установившегося значения Θ∞, если бы отсутствовала передача тепла в окружающую среду и все выделяемое тепло накапливалось в теле.
Решение уравнения нагревания
В уравнении (4) можно разделить переменные и привести его к виду
| (6) |
При интегрировании уравнения (6) получим
| t / T = – ln (Θ∞ – Θ) + C . | (7) |
Постоянная C определяется из начального условия: при t = 0 тело в общем случае имеет некоторое превышение температуры Θ = Θ0. Подставив указанные значения t и Θ в (7), найдем, что
C = ln (Θ∞ – Θ0) .
Подставим это значение C в (7) и переменим знаки. Тогда
![]()
откуда окончательно для Θ = f(t) находим
| Θ = Θ∞ × (1 – e–t/T) + Θ0 × e–t/T . | (8) |
Случай нагревания при Θ0 = 0
В этом случае вместо выражения (8) имеем
| (9) |
чему соответствует экспоненциальная кривая нагревания, изображенная на рисунке 1, а. При малых t, когда и Θ мало, теплопередача в окружающее пространство также мала, большая часть тепла накапливается в теле и температура его растет быстро, как это видно из рисунка 1, а. Затем с ростом Θ теплоотдача увеличивается и рост температуры тела замедляется. При t = ∞, согласно равенству (9), Θ = Θ∞.
На рисунке 1, а указаны значения Θ, достигаемые через интервалы времени T, 2T, 3T и 4T. Из этого рисунка видно, что тело достигает практически установившегося превышения температуры через интервал времени t = 4T.
Охлаждение тела
Если тело имеет некоторое начальное превышение температуры Θ ≠ 0, но Q = 0 и, следовательно, в соответствии с выражением (2) Θ∞ = 0, то происходит охлаждение тела от Θ = Θ0 до Θ = Θ∞ = 0.
Подставив в (8) Θ∞ = 0, получим уравнение охлаждения тела
| (10) |
Экспоненциальная кривая охлаждения тела согласно уравнению (10) представлена на рисунке 1, б. Сначала, когда Θ и соответственно также теплоотдача велики, охлаждение идет быстро, а по мере уменьшения Θ охлаждение замедляется. При t = ∞ будет Θ = 0.
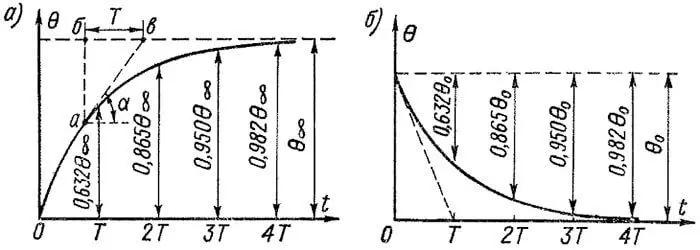
Рисунок 1. Кривые нагревания (а) и охлаждения (б) идеального однородного твердого тела
Общий случай нагревания тела
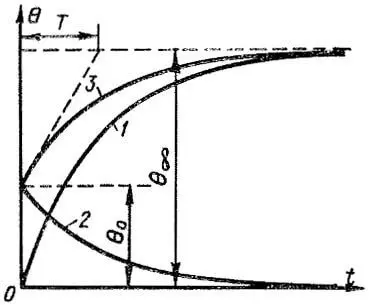 |
| Рисунок 2. Общий случай нагревания идеального однородного твердого тела |
Общий случай нагревания тела, описываемый уравнением (8), на основании формул (9) и (10) можно рассматривать как наложение двух режимов: 1) нагревания тела от начального превышения температуры Θ = 0 до Θ = Θ∞ и 2) охлаждения тела от Θ = Θ0 до Θ = 0. На рисунке 2 кривая 3 представляет собой кривую нагревания, построенную по уравнению (8). Эту кривую можно получить путем сложения ординат кривых 1 и 2, соответствующих уравнениям (9) и (10).
Графический способ определения T
Найдем подкасательную бв (рисунок 1, а), отсекаемую на асимптоте Θ = Θ∞ касательной к кривой Θ = f (t). Из рисунка 1, а следует, что
| (11) |
где α – угол наклона касательной к кривой Θ = f(t).
Как известно,
![]()
Но, согласно выражению (6),
| (12) |
Подставив tg α из (12) в (11), получим
бв = T .
Таким образом, подкасательная к любой точке кривой нагревания или охлаждения равна постоянной времени нагревания T. Этим свойством кривых Θ = f(t) можно воспользоваться для графического определения T, если имеется кривая Θ = f(t), снятая, например, опытным путем. На рисунке 1, б и 2 показан способ определения T при построении касательной к начальной кривой.
Заключительные замечания
Выше была изложена теория нагревания идеального однородного твердого тела. В действительности электрическая машина не представляет собой такого тела, так как она состоит из разных частей, обладающих конечной теплопроводностью, причем теплопроводность электрической изоляции достаточно мала. Поэтому отдельные части машины (обмотка, сердечники и другие) имеют различные температуры. В связи с этим более правильно было бы рассматривать электрическую машину как совокупность нескольких однородных тел, между которыми существует теплообмен. В действительных условиях величина T также не вполне постоянна, так как коэффициенты теплоотдачи зависят в определенной мере от температуры. Кроме того, воздух или другой охлаждающий агент при протекании по вентиляционным каналам нагревается, и поэтому температура охлаждающей среды для различных участков охлаждаемой поверхности имеет различные значения.
Таким образом, кривые нагревания и охлаждения не являются, строго говоря, экспоненциальными. Однако в большинстве практических случаев мы не делаем существенных ошибок, считая их экспоненциальными, то есть применяя изложенную выше теорию нагревания идеального однородного тела.
Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.